В 1966 г. Папа разрешил католикам есть мясо по пятницам. Поэтому при рассмотрении модели ежегодного спроса на рыбу в США в 1946-1970 гг. в состав регрессоров была включена фиктивная переменная Dt, так что

В 1966 г. Папа разрешил католикам есть мясо по пятницам. Поэтому при рассмотрении модели ежегодного спроса на рыбу в США в 1946-1970 гг. в состав регрессоров была включена фиктивная переменная Dt, так что модель, оцененная по данным за этот период, имела вид:

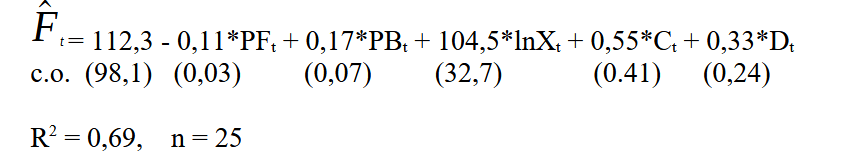
Здесь:

Ft - потребление рыбы на душу населения в год t в фунтах;

PFt - индекс цены рыбы в год t в пунктах;

PBt - индекс цены говядины в год t в пунктах;

Xt - реальный располагаемый доход на душу в год t в тысячах долларов;

Ct - число католиков в США в год t в десятках тысяч человек;

Dt - фиктивная переменная, равная 0 для периода до 1966 г., и равная 1 после.

Запишите теоретическую модель для этого выборочного уравнения.
Проинтерпретируйте коэффициент при lnXt.
Проинтерпретируйте значение коэффициента детерминации.
Значимо ли отличен от нуля коэффициент при переменной Dt?
Можно ли утверждать, что теоретический коэффициент при переменной PFt отрицательный? (левосторонний тест на ноль)
Можно ли утверждать, что истинный коэффициент при переменной PBt больше 0,1?
Провести тест на общую значимость модели.