Условие:
Найти оптимальную цену единицы товара по результатам наблюдений.
В каждом варианте задано 10 пар данных, на основе которых, используя линейную модель регрессии, требуется:
- методом наименьших квадратов определить оценки параметров модели α и β по приведенным формулам;
- определить выручку или доход (в зависимости от номера варианта) как функцию F(P) для каждой пары наблюдений;
- найти значение оптимальной цены Р, при котором доход будет максимальным (для этого возьмите производную по Р от функции F(P) и приравняйте ее 0). Из полученного выражения определяем оптимальное значение цены Р.
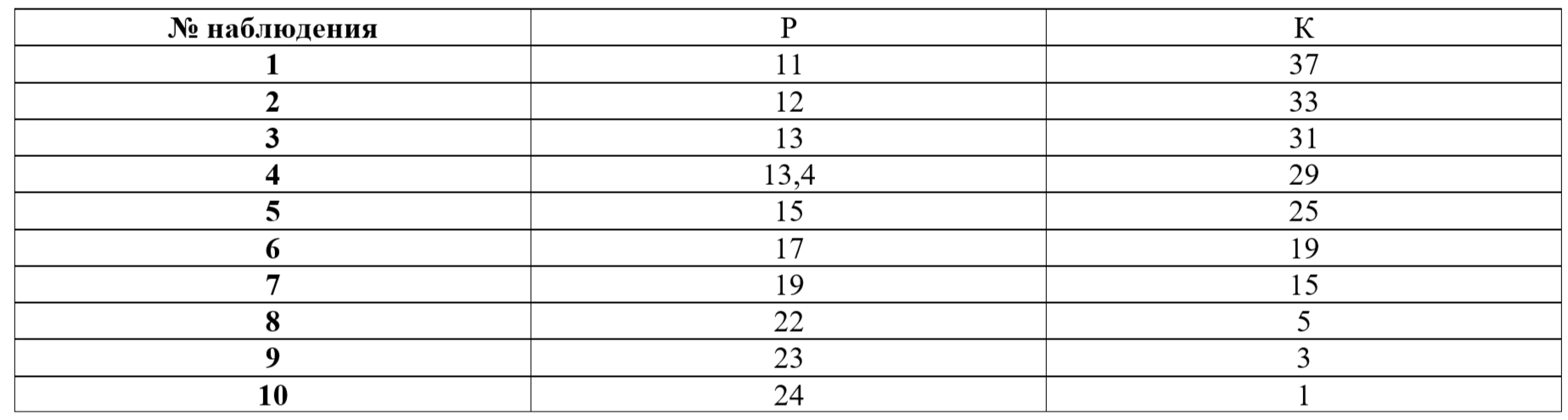
Даны: стоимость единицы товара Р и количество (шт.) проданного товара К для 10 наблюдений и расходы на рекламу А.
Используя линейную модель Ki=α+βPi+εi, найдите оптимальную цену, при которой получается максимальный доход от продаж (за вычетом затрат на рекламу).
А = 20
Таблица 1
Решение:
Значения оценок параметров для линейной модели методом наименьших квадратов вычислим по формулам:
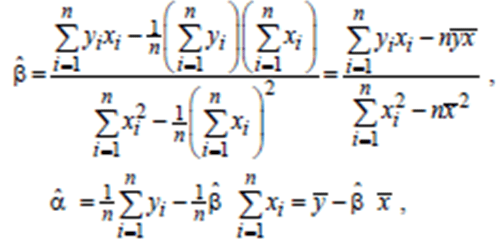
Для этого построим расчетную таблицу 2.
Таблица 2
