Решение задачи
Решить задачу линейного программирования графическим методом. Z(X)=2x_1+x_2→min Z(X)=2x_1+x_2→min {x_1+x_2≤12 (1) 2x_1-x_2≤12 (2) 2x_1-x_2≥0 (3) 2x_1+x_2≥4 (4)) x_2≥0.
- Экономика
Условие:
Решить задачу линейного программирования графическим методом.
Z(X) = 2x1 + x2→min
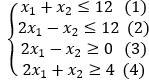
x2 ≥ 0.
Решение:
Строим область допустимых решений.
В прямоугольной декартовой системе координат (рис. 3) строим прямую x1+x2=12 (L1), соответствующую ограничению (1). Находим, какая из двух полуплоскостей, на которые эта прямая делит всю координатную плоскость, является областью решений неравенства (1). Так как прямая L1 не проходит через начало координат, то подставляет координаты точки О(0,0) в первое ограничение 0+012, строгое неравенство 012. Следовательно, точка О лежит в полуплоскости решений. Таким образом, стрелки на концах прямой (L1) должны быть направлены в полуплоскость, содержащую точку О. Аналоги...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
Р
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э