В таблицах даны оценки N альтернатив по M критериям, чем выше оценка, тем лучше альтернатива. 1. Постройте матрицу парных сравнений этих альтернатив и найдите эффективные.
- Экономика
Условие:
В таблицах даны оценки N альтернатив по M критериям, чем выше оценка, тем лучше альтернатива.
1. Постройте матрицу парных сравнений этих альтернатив и найдите эффективные.
2. Нормализуйте таблицы с оставшимися эффективными альтернативами.
3. Найдите наилучшее решение, используя принцип абсолютной уступки.
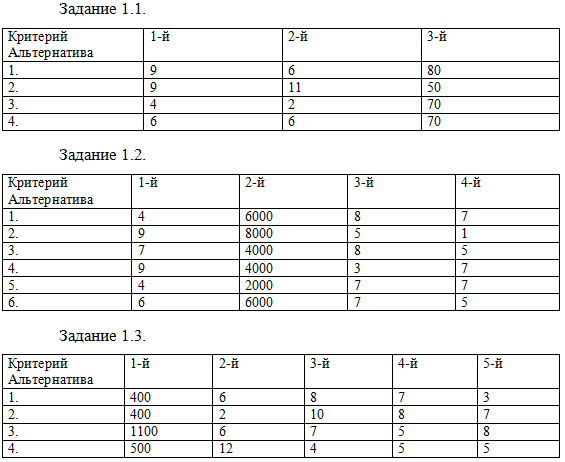
Решение:
1.1. Для решения задачи необходимо построить матрицу сравнения альтернатив (это квадратная матрица, число строк и столбцов которой равно числу сравниваемых альтернатив), в которой в i-й строке, j-м столбце будем ставить 1, если i-я альтернатива доминирует j-ю (то есть первая превосходит вторую хотя бы по одному критерию, а по остальным не уступает ей), в остальных случаях ставим 0. Исходя из этой матрицы, найти эффективные альтернативы можно убрав те альтернативы, в столбцах которых встречается хотя бы одна единица. Альтернативы, у которых в столбцах отсутствуют единицы, и будут являться эффек...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства