Условие задачи
Владелец мебельной фабрики рассматривает возможность ввода на своем предприятии сверхурочной работы и хочет оптимизировать использование этого дополнительного времени. Фирма выпускает пять различных изделий: стулья, столы, бюро, книжные шкафы, и сервировочные тележки. Соответствующая прибыль за единицу - $ 16, $ 30, $ 40, $ 42, и $ 32. Продукция требует одних и тех же основных операций: обрезка, шлифовка и отделка и сборка. Необходимое для выполнения этих операций время для каждого их изделий приведено в таблице.
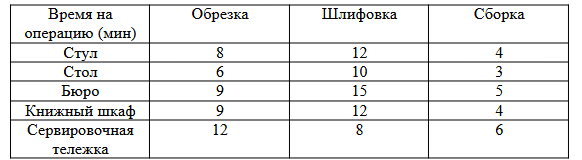
Имеется 320 мин. для обрезки, 400 для отделки, и 270 для сборки в планируемое сверхурочное время.
a. Какая комбинация изделий должна быть произведена в это время, чтобы максимизировать прибыль? Какой будет общая прибыль?
b. Если имеется изделие, которое не выгодно производить, что нужно изменить, чтобы его производство стало выгодным? Можно ли изменить что-то в технологии или в ценах так, чтобы все изделия стали выгодными? Опишите результаты.
c. Вы можете установить 100 сверхурочных минут, но только для одной из основных операций. На какую операцию стоит выделить это время? Сколько при этом получится прибыли? Подтвердите все ваши ответы вычислениями.
Ответ
Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.
Определим максимальное значение целевой функции F(X) = 16x1+30x2+40x3+42x4+32x5 при следующих условиях-ограничений.
8x1+6x2+9x3+9x4+12x5320
12x1+10x2+15x3+12x4+8x5400
4x1+3x2+5x3+4x4+6x5270
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
В 1-м неравенстве смысла () вводим базисную переменную x6. В 2-м неравенстве смысла () вводим базисную переменную x7. В 3-м неравенстве с...
