Дана схема электрической цепи с двумя источниками гармонических ЭДС: e1(t) = E1msin(314t + ψe1) и e2(t) = E2msin(314t + ψe2). Действующие значения и начальные фазы ЭДС приведены в исходных данных. Заданы значения параметров схемы (см.исходные данные).
- Электроника, электротехника, радиотехника
Условие:
Дана схема электрической цепи с двумя источниками гармонических ЭДС: e1(t) = E1msin(314t + ψe1) и e2(t) = E2msin(314t + ψe2). Действующие значения и начальные фазы ЭДС приведены в исходных данных. Заданы значения параметров схемы (см.исходные данные).
Требуется выполнить следующий объем расчетов:
Подсчитать комплексные сопротивления и проводимости ветвей. Индекс сопротивления равен индексу тока. Записать комплексы ЭДС источников. Составить комплексную схему замещения. На схеме должны быть указаны комплексные сопротивления, комплексы токов и ЭДС ветвей.
Определить токи в ветвях комплексной схемы замещения методом контурных токов. Осуществить проверку полученных результатов с помощью второго закона Кирхгофа.
Определить токи в ветвях комплексной схемы замещения методом двух узлов. Осуществить проверку полученных результатов с помощью первого закона Кирхгофа.
Проверить выполнение баланса активных и реактивных мощностей. С этой целью подсчитать отдельно комплексные мощности источников и приемников энергии и сравнить их вещественные и мнимые части (т.е. активные и реактивные мощности). Погрешность расчета не должна превышать 2%. Записать уравнение баланса мощностей с помощью матричного соотношения.
Построить на комплексной плоскости векторную диаграмму комплексных потенциалов и векторную диаграмму токов в ветвях схемы.

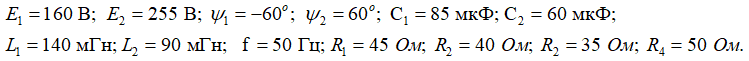
Решение:
1. Расчет сопротивлений.
Определим сопротивления реактивных элементов на частоте 50 Гц
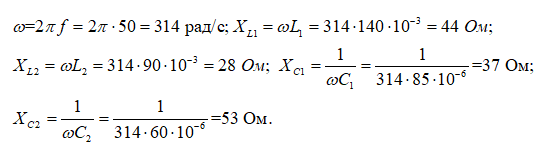
Переходим к комплексной схеме замещения.
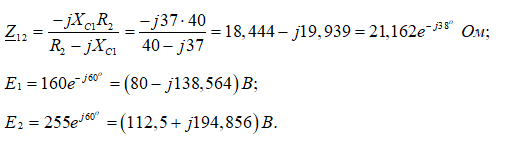
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства