На однозвенную полнодоступную КС емкостью 10 линий поступает простейший поток вызовов с параметрами 120, 300 вызовов в час. Среднее время обслуживания 80 сек. Требуется определить интенсивность нагрузки, обслуживаемой пучком линий.
- Электроника, электротехника, радиотехника
Условие:
На однозвенную полнодоступную КС емкостью υ = 10 линий поступает простейший поток вызовов с параметрами λ1 = 120, λ2 = 300 вызовов в час. Среднее время обслуживания t = 80 сек. Вызовы обслуживаются в системе с явными потерями. Требуется определить:
• Вероятность того, что в произвольный момент времени в системе занято точно i линий (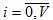 );
);
• Среднее число занятых линий – М[i];
• Построить графики зависимости Pi=f(i);
• Потери по вызовам – Рв, нагрузке – Рн, времени – Рt;
• Интенсивность нагрузки, обслуживаемой пучком линий.
Решение:
Вероятности Pi в данной модели определяются первой формулой Эрланга
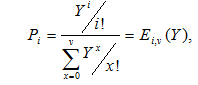
где
Y интенсивность поступающей нагрузки, Y = t.
Определим величины Pi для 1 = 120 выз/час. Для этого целесообразно воспользоваться рекуррентной формулой:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства