Найти коэффициент «а» аппроксимирующего выражения, используя метод наименьших квадратов. Построить в системе декартовых координат кривые намагничивания.

Электрическая цепь (рис. 3) содержит катушку с ферромагнитным сердечником. Кривая намагничивания сердечника для положительных значений индукции и напряженности магнитного поля задана в виде таблицы (табл. 2). При этом пренебрегают явлениями гистерезиса и не учитывают вихревые токи, не учитываются явления рассеивания. Предполагается также, что индукция в сердечнике изменяется по синусоидальному закону.

Таблица 2 – Кривая намагничивания

Параметры элементов схемы, максимальная величина магнитной индукции В_m, длина l средней магнитной линии и поперечное сечение S сердечника для различных вариантов (исходные данные) приведены в табл. 4. Значения индуктивного X_L, и емкостного Х_C сопротивлений соответствуют частоте f, указанной в этой же таблице.

Аппроксимирующее выражение кривой намагничивания:

Н = а ∙ В³ (1)

В задаче требуется:

1. Найти коэффициент «а» аппроксимирующего выражения,  используя метод наименьших квадратов. Построить в одной и той же системе декартовых координат кривые намагничивания по полученному аппроксимирующему выражению и заданной таблице.

2. При этом построение выполнить как для положительных, так и для отрицательных значений В и Н. Качественно сопоставить построенные кривые.

3. В одной и той же системе декартовых координат построить кривые изменения тока источника энергии i и приложенного к цепи напряжения u 

источника энергии от времени, т.е. кривые мгновенных значений тока и напряжения источника: i = i (t) и u = u (t).

4. Определить показания приборов, считая, что вольтметр и амперметр имеют электромагнитное измерительное устройство, а ваттметр – электродинамическое.

Исходные данные

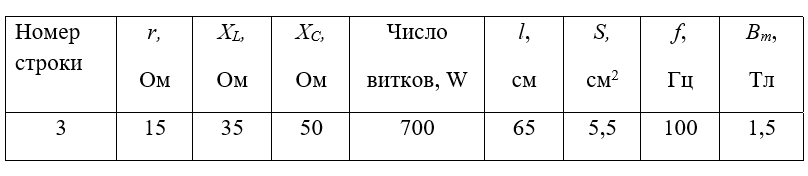
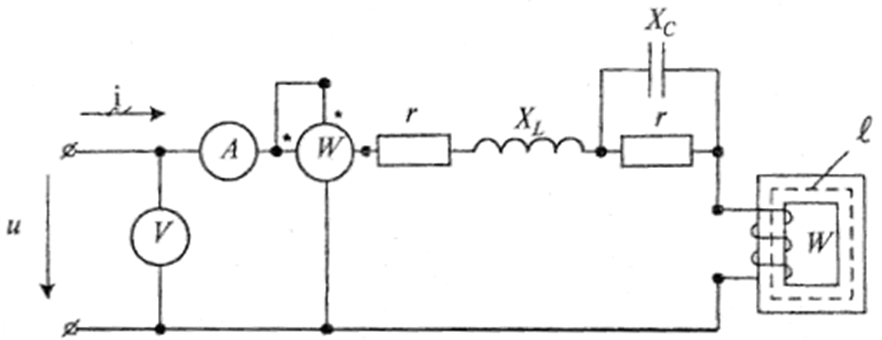
Рис. 3