Условие задачи
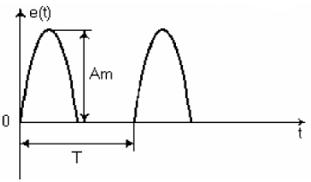
1. Перечертить схему электрической цепи и кривую несинусоидальной ЭДС.
2. Указать вид симметрии кривой и установить, какие гармонические составляющие должны содержаться в ее разложении.
3. Разложить кривую ЭДС на гармоники в ряд Фурье и записать аналитическое выражение разложения, учитывая постоянную составляющую первую, вторую, пятую и седьмую гармоники.
4. Рассчитать по данным разложения коэффициенты искажения и несинусоидальности для периодических кривых.
5. Построить схемы замещения исходной электрической цепи для каждой учитываемой гармоники ЭДС в отдельности, включая схему для постоянной составляющей, если такая имеется в разложении.
6. Для заданных L,C параметров рассчитать сопротивления ветвей на частоте каждой гармоники в отдельности и найти токи во всех ветвях для всех схем замещения, а затем найти действительные несинусоидальные токи и падения напряжений в ветвях.
7. Определить показания измерительных приборов.
8. Рассчитать коэффициент мощности электрической цепи при периодических несинусоидальных токах, напряжениях и ЭДС, включая коэффициенты сдвига по фазе между первыми гармониками ЭДС и входного тока и коэффициент искажения мощности.
9. Рассчитать модуль полной мощности и величину активной мощности потребляемую электрической цепью, а также активную, реактивную и полную мощности по первым гармоникам.
10. Построить графики гармоник ЭДС с первой по седьмую включительно и, суммируя их, получить график несинусоидальной ЭДС, воздействующей на электрическую цепь.
11. Сравнить графики заданной и синтезированной кривой ЭДС.
Исходные данные:
Z1=20 Ом;
Z2=j22,5 Ом;
Z3=-j40 Ом;
Z4=40 Ом;
Z5=j30 Ом;
Z6=-j100 Ом;
Am=500 В;
T=0,02 с;
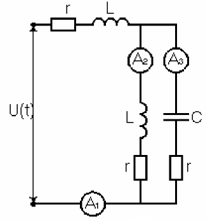
Рис. 1
Ответ
Дано:
Z1=20 Ом;
Z2=j22,5 Ом;
Z3=-j40 Ом;
Z4=40 Ом;
Z5=j30 Ом;
Z6=-j100 Ом;
Am=500 В;
T=0,02 с;
1. Найдем угловую частоту (рад/с):
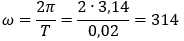
Разложение несинусоидальной кривой в ряд Фурье:
