Условие задачи
Расчет линейной цепи при несинусоидальных напряжениях и токах.
Содержание работы
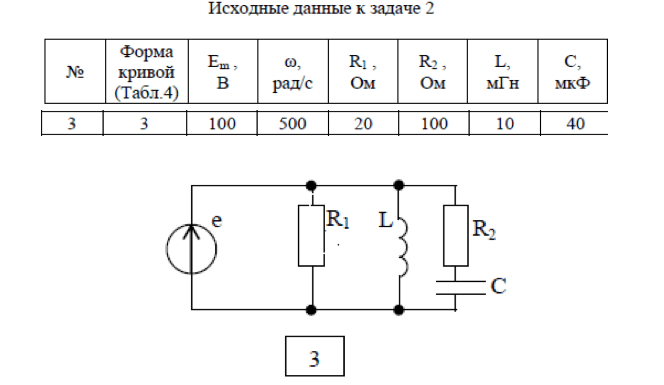
Для электрической цепи, соответствующей номеру варианта, выполнить
следующее:
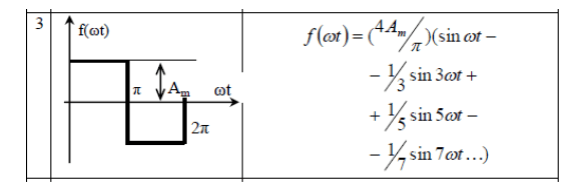
1. Разложить периодическую несинусоидальную ЭДС e = f (ωt ), заданную в виде графика, в ряд Фурье, ограничившись первыми тремя гармониками. Написать уравнение мгновенного значения ЭДС e= f (ωt )
2. Определить действующее значение несинусоидальной ЭДС.
3. Вычислить токи гармоник на неразветвленном участке цепи и записать закон изменения суммарного тока.
4. Построить в масштабе гармоники входного напряжения и их графическую сумму, а также заданную кривую (в одних осях).
5. Построить в масштабе графики гармоник входного тока и их графическую сумму.
6. Определить активную, реактивную и полную мощности, а также коэффициент мощности и коэффициент искажения.
Ответ
1. Разложить аналитически в ряд Фурье заданную периодическую несинусоидальную ЭДС е=f(t), ограничившись вычислением первых трех гармоник; написать уравнение мгновенного значения ЭДС.
Для заданной формы несинусоидальной ЭДС разложение в ряд Фурье имеет вид:
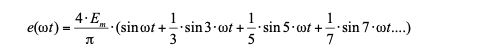
При заданном значении получаем разложение для первых трех гармоник:
