1. Главная
  2. Библиотека
  3. Электроника, электротехника, радиотехника
  4. Решить численным методом дифференциальное уравнение заряда RC-цепи с постоянной времени t от источника напряжения E, котор...

Решить численным методом дифференциальное уравнение заряда RC-цепи с постоянной времени t от источника напряжения E, которое имеет вид

«Решить численным методом дифференциальное уравнение заряда RC-цепи с постоянной времени t от источника напряжения E, которое имеет вид»
  • Электроника, электротехника, радиотехника

Условие:

Решить численным методом дифференциальное уравнение заряда RC-цепи с постоянной времени 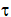от источника напряжения E, которое имеет вид 

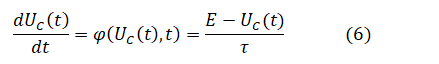
методом Эйлера и Рунге-Кутта 4 – ого порядка при постоянном шаге Δt = 0.15 и 0.5 на интервале от 0 до 2.5.

Построить на графике численное решение ДУ и аналитическое решение (5), вычислить глобальную ошибку для всех методов.

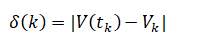
Результаты вычислений представить в виде таблицы.

Построить сравнительные графики численного решения ОДУ методом Рунге-Кутта и Эйлера на одной координатной оси при разных шагах.

Решение:

1. При решении ДУ заряда RC цепи явным методом Эйлера его рекуррентная формула выглядит следующим образом:

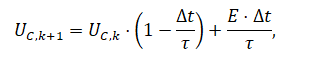
где 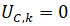начальное условие.

2. При решении ДУ заряда RC цепи методом Рунге-Кутты 4-го порядка ...

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я