Условие задачи
Постановка задач
1. Из типовых блоков на вкладке «Динамические» собрать модель системы управления и задать её параметры согласно варианту (табл. 3.1).
Если дано два звена, они соединяются последовательно. В качестве источника управляющего сигнала использовать ступенчатую функцию Хевисайда 1(t) (вкладка «Источники»). Выходной сигнал вывести на временной график (вкладка «Данные»).
2. Смоделировать отклик системы на входное воздействие в интервале времени от t = 0 до времени, в 10 раз превышающее наибольшую постоянную времени из заданных по варианту, т. е. t = 10·Tmax. Этот отклик, как реакция на входную «ступень», будет являться переходной функцией САУ. Конечное время, шаг вывода графиков и т. п. задаётся в пункте меню «Моделирование» – «Параметры расчёта». Для этого и последующих заданий рекомендуется использовать метод интегрирования Гира, а шаг вывода и шаг интегрирования установить в диапазоне 0,001…0,01 с.
3.Построить частотные характеристики системы: АФХ, ВЧХ, МЧХ, АЧХ, ЛАХ, ФЧХ.
4. Из всех заданных параметров системы уменьшить в два раза значение одной постоянной времени и одного коэффициента усиления. Снова построить переходную функцию и частотные характеристики в одном масштабе по обеим осям с полученными ранее графиками.
Ответ
Ход работы
ПФ инерционного интегрирующего звена в общем случае записывается в виде:
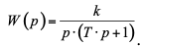
С учётом данных таблицы 3.1, запишем ПФ звена: 
С учётом того, что нужно также проводить исследования для звена с постоя...
