Условие задачи
Задан одножильный маслонаполненный кабель с заземленной свинцовой оболочкой. Длина кабеля равна l радиус токоведущей жилы r и радиус оболочки R. Изоляция кабеля имеет диэлектрическую проницаемость εr. Кабель рассчитан на напряжение U.
Требуется:
1. Рассчитать емкость кабеля.
2. Определить характер изменения напряженности электрического поля у поверхности токоведущей жилы при увеличении ее радиуса от r до R.
3. Определить распределение потенциала в толще изоляции при неизменном радиусе внутренней жилы r.
4. Построить рассчитанные зависимости Е=f(х), φ=f(х). Числовые данные для каждого варианта приведены в табл. 2.15.
Исходные данные:
Напряжение кабеля U=115кВ.
Радиус оболочки R=18мм.
Радиус токоведущей жилы r=2мм.
Длина кабеля l=1400м.
Диэлектрическая проницаемость εr=3,75.
Ответ
1. Рассчитаем емкость кабеля.
Если рассматривать кабель как цилиндрический конденсатор, то его емкость определится по формуле
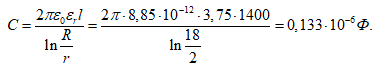
2. Определим характер изменения напряженности электрического поля у поверхности токоведущей жилы при увеличении ее радиуса от r до R.
По теореме Гаусса напряженность электрического поля цилиндрического конденсатора в слое с радиусом rх равна









