Условие задачи
Катушка (без сердечника) длиной ℓ и с площадью поперечного сечения S1 имеет N плотно навитых витков. Катушка соединена параллельно с конденсатором, состоящим из двух пластин площадью S2 каждая, расстояние между пластинами равно d. Диэлектрик- воздух. Максимальное напряжение на пластинах конденсатора равно Umax и соответствует времени t = 0.
1) Определить период колебаний в контуре (сопротивлением контура пренебречь).
2) На какую длину электромагнитной волны λ резонирует контур?
3) Найти мгновенный ток i(t) в контуре.
4) Определить максимальное значение объемной плотности энергии ωm магнитного поля катушки.
5) Зная ωm, найти максимальное значение объемной плотности энергии ωc электрического поля конденсатора.
Исходные данные:
S1 = 4.5 см2 = 4,5∙10-4 м2
S2 = 75 см2 = 75∙10-4 м2
ℓ =58 см = 0,58 м
d = 5,2 мм = 5,2∙10-3 м
N = 900
Umax = 20 В
Ответ
Дано:
S1 = 4.5 см2 = 4,5∙10-4 м2
S2 = 75 см2 = 75∙10-4 м2
ℓ =58 см = 0,58 м
d = 5,2 мм = 5,2∙10-3 м
N = 900
Umax = 20 В
Найти:
Т, , m(max), С(max)
Решение:
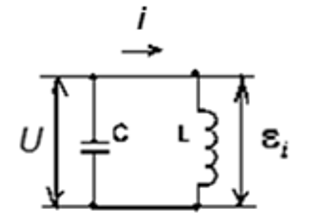
Имеется идеальный колебательный контур, изображённый на рисунке.
Контур состоит из ёмкости С и индуктивности L, омическим сопротивлением пренебрегаем (R = 0).
1) Период электромагнитных колебаний в контуре определяется формулой Том...
