Требуется:используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r.

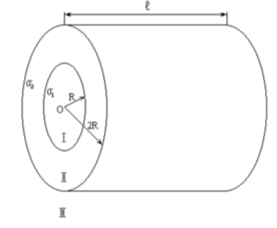
На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями s₁ и s₂ (см. рис.). Требуется: 1)используя теорему Остроградского-Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять s₁=-2s, s₂=4s; 2) вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора Е. Принять s=10нКл/м², r=3R; 3)построить график Е(r).

σ₁ = -2σ

σ₂ = 4σ

σ = 10 нКл/м² = 1·10^–8 Кл/м²

r = 3R