Условие задачи
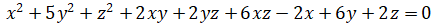
1. Привести уравнение поверхности 2 порядка к каноническому виду, используя теорему приведения квадратичной формы к главным осям, определить её тип.
2. Найти соответствующую каноническую декартову систему координат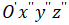 
: найти координаты точки 
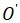(начало координат системы 
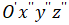) и уравнение осей координат 
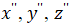в исходной системе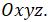 
3. Построить чертеж в канонической системе координат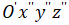 
, с указанием осей координат.
4. Найти центр или множество центров как решение матричного уравнения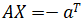 
(было выведено в лекции). Проверить, что найденные в п.2 координаты точки 
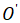совпадают с координатами его центра (если он один), или что точка 
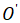принадлежит множеству центров (если их много). Если матричное уравнение решение не имеет, проверить, что данная поверхность принадлежит классу поверхностей, не имеющих центра.
5. Обосновать данный метод приведения уравнения поверхности 2 порядка к каноническому виду.
Ответ
Итак, для приведения поверхности второго порядка, заданной в прямоугольной системе координат, к каноническому виду нужно выполним следующие действия.
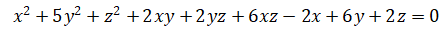
Это уравнение вида
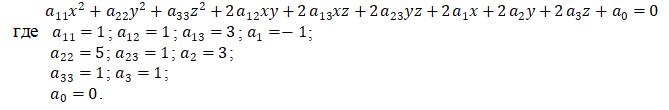
Составим матрицу квадратичной фун...
