Прямоугольник, стороны которого равны a и b, вращается вокруг оси, перпендикулярной его диагонали и проходящей через один из её концов. Найти площадь поверхности полученного тела вращения.
«Прямоугольник, стороны которого равны a и b, вращается вокруг оси, перпендикулярной его диагонали и проходящей через один из её концов. Найти площадь поверхности полученного тела вращения.»
- Геометрия
Условие:
Прямоугольник, стороны которого равны a и b, вращается вокруг оси, перпендикулярной его диагонали и проходящей через один из её концов. Найти площадь поверхности полученного тела вращения.
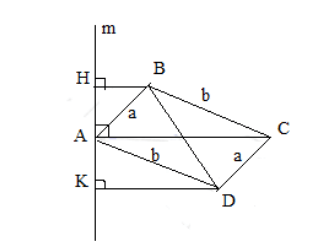
Дано: АВСД-прямоугольник.
АВ=СD=а
ВС=АD=b
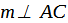
Найти: 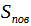
Решение:
Проведем перпендикуляры BH, CF, DK на прямую m (ось вращения). Тогда площадь поверхности тела вращения равна:
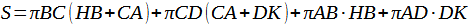
По теореме Пифагора
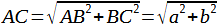
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э