Условие задачи
Истечение происходит из открытого резервуара при постоянном напоре воды Н1 по короткому трубопроводу переменного поперечного сечения с диаметрами d1 и d2 в атмосферу и из конически расходящегося насадка с диаметром выходного сечения dн и длиной lн = 5 dн под уровень (рис. 5.4). Разность уровней − Н2 = 1,5 м.
На втором участке трубопровода имеются два колена с плавным поворотом, коэффициент сопротивления каждого ξк = 0,15, и задвижка, коэффициент сопротивления которой ξз = 8,0. Коэффициент гидравлического трения на первом участке длиной l1 принять равным λ1= 0,04, на втором участке длиной l2−λ 2 = 0,025.
Определить:
1.Скорость истечения ν2 и расход Q2 через трубопровод.
2.Скорость истечения и расход через затопленный конически расходящийся насадок, если коэффициент скорости и коэффициент расхода насадка равны и составляют φн = μн = 0,45.
3. Сравнить скорость и расход через насадок со скоростью и расходом через отверстие в тонкой стенке того же диаметра. Коэффициент скорости для отверстия φ = 0,97, а коэффициент расхода μ = 0,62.
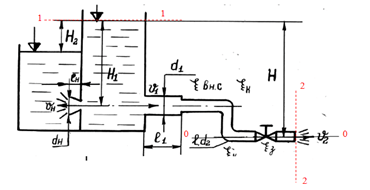
ν2, Q2, Qн = ?
Ответ
Дано: d1 = 400 мм = 0,4 м, d2 = 100 мм = 0,1 м, l1 = 0,8 м,l2 = 2 м, dн = 200 мм = 0,2 м, Н = 6 м, Н1 = 5 м.
1.Запишем уравнение Бернулли для сечений 1-1 и 2-2 относительно плоскости сравнения 0-0, и найдем скорость истечения 2 и расход Q2 через трубопровод.
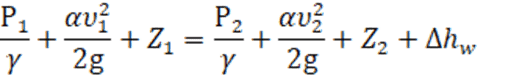
где - удельный вес воды, Н/м;
