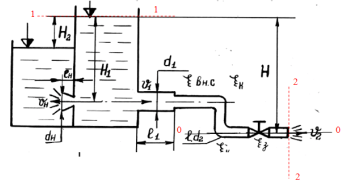
Истечение происходит из открытого резервуара при постоянном напоре воды Н1 по короткому трубопроводу переменного поперечного сечения диаметрами d1 и d2 в атмосферу и из конически расходящегося насадка диаметром выходного сечения
- Гидравлика
Условие:
Истечение происходит из открытого резервуара при постоянном напоре воды Н1 по короткому трубопроводу переменного поперечного сечения диаметрами d1 и d2 в атмосферу и из конически расходящегося насадка диаметром выходного сечения dн и длиной lн = 5 dн под уровень (рис. 5, г). Разность Уровней H2 = 1,5 м.
На втором участке трубопровода имеются два колена с плавным поворотом, Коэффициент сопротивления каждого 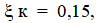 и задвижка, коэффициент сопротивления которой
и задвижка, коэффициент сопротивления которой 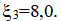 Коэффициент гидравлического трения на первом участке длиной l1 принять равным
Коэффициент гидравлического трения на первом участке длиной l1 принять равным 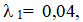 на втором участке длиной l2 принять
на втором участке длиной l2 принять 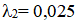
Определить:
1) скорость истечения V2 и расход Q2 через трубопровод;
2) скорость истечения и расход через затопленный конически расходящийся насадок, если коэффициент скорости и коэффициент расхода для насадка равны и составляют 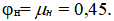
Сравнить скорость и расход через насадок со скоростью и расходом через отверстие в тонкой стенке того же диаметра. Коэффициент скорости для отверстия 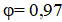 , а коэффициент расхода
, а коэффициент расхода 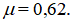
Решение:
Дано:
d1 = 400 мм = 0,4 м, d2 = 100 мм = 0,1 м, l1 = 0,8 м,l2 = 2 м, dн = 200 мм = 0,2 м, Н = 6 м, Н1 = 5 м.
Найти:
2, Q2, Qн = ?
1. Запишем уравнение Бернулли для сечений 1-1 и 2-2 относительно плоскости сравнения 0-0, и найдем скорость истечения 2 и расход Q2 через трубопровод.
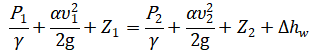
где удельный вес воды, Н/м;
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства