Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа А формула тождественно истинна?

1) введём обозначения A = ДЕЛ(x, А), D21 = ДЕЛ(x, 21) , D35 = ДЕЛ(x, 35)

2) введём множества:

A множество натуральных чисел, для которых выполняется условие A

D₂₁ множество натуральных чисел, для которых выполняется условие D₂₁

D₃₅ множество натуральных чисел, для которых выполняется условие D₃₅

3) Запишем формулу из условия в наших обозначениях

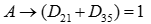
4) Раскроем импликацию по правилу