Условие:
Сколько различных решений имеет система логических уравнений
(x1 → x2) = 1
(y1 → y2 → y3) = 1
(z1 → z2 →z3 →z4) = 1
(x1 → y1) ∧ (y3→ z3) = 1
где x1, x2, y1, …, y3, z1, …, y4 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполняются данные равенства. В качестве ответа нужно указать количество таких наборов.
Решение:
Импликация ложна только тогда, когда первый аргумент равен 1, а второй равен 0. Составим таблицу истинности для выражения x1 x2.
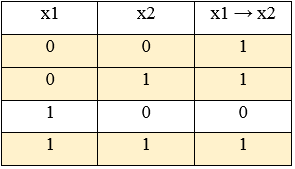
Из таблицы видно, что уравнение x1 x2 = 1 имеет три решения, строки с которыми в таблице выделены.
Аналогичным образом составим таблицу истинности для двух других уравнений. Значения импликаций будем вычислять по очереди, слева направо, используя правило A B С ...
