Главная
Библиотека
Картография и геоинформатика
1. На сетке проекции Меркатора через заданные точки А и В построить линии положения: локсодромию и ортодромию. 1. Построе...

1. На сетке проекции Меркатора через заданные точки А и В построить линии положения: локсодромию и ортодромию. 1. Построение лини и положения

«1. На сетке проекции Меркатора через заданные точки А и В построить линии положения: локсодромию и ортодромию. 1. Построение лини и положения»

4 декабря 2024
Картография и геоинформатика

Условие:

1. На сетке проекции Меркатора через заданные точки А и В построить линии положения: локсодромию и ортодромию.
2. Вычислить длину локсодромии и ортодромии, а также площадь участка, ограниченного крайними меридианами и параллелями.
3. Измерить длину локсодромии и площадь участка.
Локсодромия - линия, пересекающая все меридианы под постоянным углом.
Ортодромия - кратчайшее расстояние между двумя точками на поверхности шара.

Исходные данные:

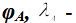координаты точки А\

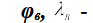координаты точки В\

R - средний радиус кривизны, который выбирается из картографических таблиц [см. приложение] по значению φк = (φю + φс) /2.

ПОРЯДОК ВЫПОЛНЕНИЯ:
Возьмем следующие значения исходных данных:

Решение:

1. Построение лини и положения

1.1. Построение локсодромии
Проекция Меркатора обладает свойством локсодромичности, т.е. локсодромия в ней изображается прямой линией.
Нанесем на сетку проекции Меркатора точки А и В по их географическим координатам. Соединив их прямой линией, получим локсодромию (рис.2).

1.2. Построение ортодромииЧтобы построить ортодромию, необходимо вычислить географические координаты ее промежуточных точек. Для упрощения задачи можно вычислить координаты орт i точек, лежащих на меридианах картографической сетки .

Не нашел нужную задачу?