Определить узел транспортной сети прямоугольной конфигурации, в котором размещение распределительного склада обеспечит минимум грузооборота транспорта по доставке грузов в обслуживаемую сеть.

24 января 2025
Логистика

Условие:

На территории района (рисунок 1.) имеется 8 магазинов, торгующих продовольственными товарами. Реальные дороги нанесены слабым пунктиром.

На рисунке сплошными линиями нанесена также абстрактная транспортная сеть прямоугольной конфигурации, состоящая из вертикальных дорог (а, б, в ... и) и горизонтальных дорог (1, 2, 3 ... 8). Задание заключается в том, чтобы найти узел абстрактной транспортной сети (перекресток), размещение в котором склада обеспечит минимум грузооборота транспорта по доставке грузов в обслуживаемую сеть.

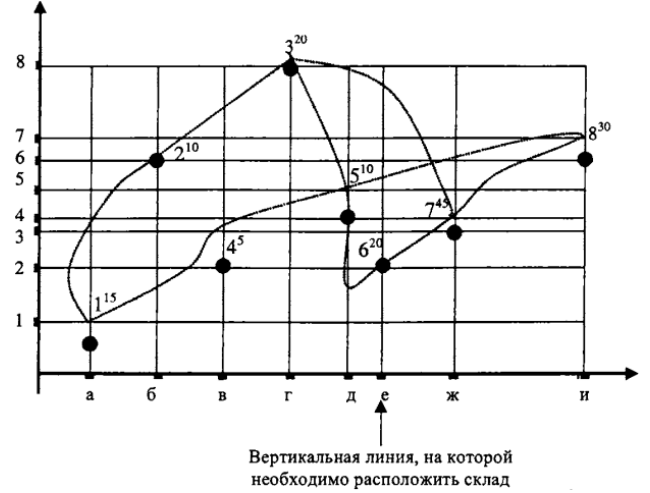
Рисунок 1. Определение оптимального места расположения распределительного склада в условиях прямоугольной сети автомобильных дорог

Решение:

В нашем случае обслуживаемая система состоит из восьми потребителей (рисунок 1., справа от потребителей указан их месячный грузооборот). Сеть дорог прямоугольная. Присваивая абсциссам потребителей соответствующие значения грузооборота, найдем методом пробной точки координату Х оптимального узла транспортной сети.

Очевидно, что абсциссой оптимального узла является точка "е". Действительно, на отрезке д-е левый грузооборот пробной точки составит 15 + 10 + 5 + 20 + 10 = 60 т/мес., а правый грузооборот - 20 + 45 + 30 = 95 т/мес. Правый больше левого, следовательно, перемещаемся на следующий отрезок...