Условие задачи
Дано:
F2 = 50 кН; M2 = 130 кН·м; b = 2 м; с = 2 м; [σ] = 160 МПа.
Требуется:
1. Построить эпюры поперечных сил Q и изгибающих моментов М.
2. Подобрать двутавровое и круглое сечение балки.
3. Проверить прочность подобранного сечения.
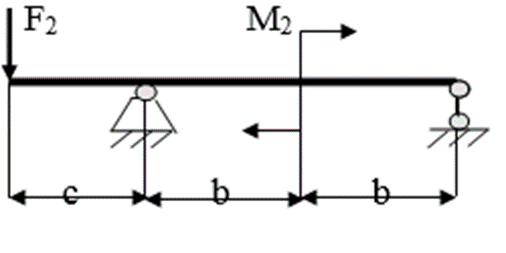
Рис.6.1 - Схема балки
Ответ
Определяем опорные реакции.
Заменяем связи реакциями: в подвижном шарнире В - RB , в неподвижном шарнире A - XA , YA. Для полученной плоской системы сил составляем три уравнения равновесия:
Fix = XA = 0, (1)
MA = 0, F2c - M2 + RB2b = 0, (2)
MВ = 0, F2(c + 2b) - M2 - YA2b = 0, (3).
Из уравнения (2), находим:
RB = (- F2c + M2 )/2b = (- 502 + 130)/22 = 7,5 кН.
Из уравнения (3), имеем:
YA = [F2(c + 2b) - M2]/2b = [50(2+22) - 130]/22 = 42,5 кН.
Проверяем правильность определения опорных реакций.
Должно выполнять условие равновесия: Fiу = 0
Fiу = YA + RB - F2 = 42,5 + 7,5 - 50 = 50 - 50 = ...
