1. Главная
  2. Библиотека
  3. Механика
  4. Для заданной расчетной схемы (рис.3) необходимо: 1. Показать на расчетной схеме реакции опор и определить их величину. 2...

Для заданной расчетной схемы (рис.3) необходимо: 1. Показать на расчетной схеме реакции опор и определить их величину. 2. Составить уравнение поперечной силы Q(x) и изгибающего момента  М(х) для всех участков.

«Для заданной расчетной схемы (рис.3) необходимо: 1. Показать на расчетной схеме реакции опор и определить их величину. 2. Составить уравнение поперечной силы Q(x) и изгибающего момента  М(х) для всех участков.»
  • Механика

Условие:

Для заданной расчетной схемы (рис.3) необходимо:

1. Показать на расчетной схеме реакции опор и определить их величину.

2. Составить уравнение поперечной силы Q(x) и изгибающего момента  М(х) для всех участков. Построить эпюры изменения поперечной силы Q(x) и изгибающего момента М(х) по длине балки.

3. Из построенной эпюры изгибающего момента М(х) найти его максимальное по модулю значение. Из условия прочности определить размеры поперечного сечения балки и сравнить его по погонной массе с двутавром. 

Исходне данные:

Р = 3 кН, q = 5 кН/м,  М = 6 кН*м, a = 2м, b = 4м, [ σ ] = 120 МПа, сечение – квадрат.

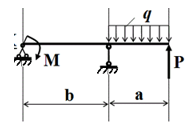
Рис.3 Схема балки 

Решение:

1. Построим балку согласно исходных данных (рис.4а).

2. Определим реакции в опорах.

Для определения реакции в шарнирно-подвижной опоре приравниваем сумму моментов всех сил относительно точки 1 к нулю.

М1 =0; Р * 6 - q * 2 * 5 - М + R2 * 4 = 0;

R2 = (- Р * 6 + q * 2 * 5 + М) / 4 = (- 3 * 6 + 5 * 2 * 5 + 6) / 4 = 9,5 кН.

Для определения реакции в шарнирно-неподвижной опоре приравниваем сумму моментов всех сил относительно точки 2 к нулю.

М2 =0; Р * 2 - q * 2 * 1 - М + R1 * 4 = 0;

R1 = (- Р * 2 + q * 2 * 1 + М) / 4 = (- 3 * 2 + 5 * 2 * 1 + 6) / 4 = 2,5 кН.

Проверка: R2 + Р q * 2 - R1 = 9,5 + 3 5...

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я