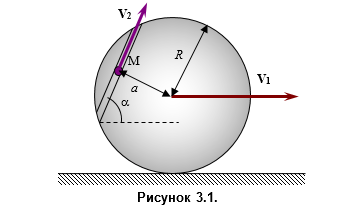
По горизонтальной дороге катится колесо радиуса R со скоростью V1. В колесе имеется прямолинейный желоб с центром на расстоянии a от оси колеса. По желобу движется точка M со скоростью V2 относительно колеса.
Определить: направление скорости точки относительно дороги и модуль этой скорости в момент, когда желоб находится под углом α к горизонту, а точка находится в центре желоба (см. рисунок 3.1).
V1= 38м/с, V2= 13м/с, = 25, R = 7м, а = 5 м.
Рассматриваем движение точки как сложное. состоящее:из переносного (вращательное) вместе с колесом относительно мгновенного центра скоростей (точка К) и относительного - прямолинейное со скоростью V2 вдоль желоба. Согласно теореме о сложении скоростей можно записать:
, или (1), где V3 = МК = L, (2). Угловая скорость качения колеса равна: = V/R = 38/7 = 5,43 рад/с. Расстояние L, определяем с помощью теоремы косинусов для треугольника СМК.