Монета подбрасывается n=1000 раз. Пусть Х – число выпавших гербов – случайная величина. Определите интервал возможных значений Х, симметричный относительно математического ожидания, внутри которого Х находится с вероятностью Р=0,997.

Для решения задачи воспользуемся интегральной теоремой Муавра-Лапласа. В нашем случае имеем:

- число измерений n = 1000;

- вероятность появления события p = 0.5;

- вероятность того, что событие не произойдет q = 1 - 0.5 = 0.5;

- границы интервала (a; b).

Определяем соответствующие величины:

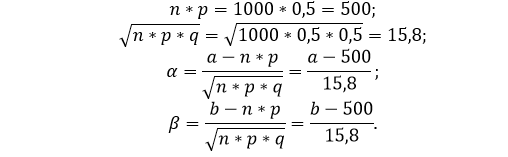
Вероятность того, что Х примет знач...