Условие задачи
Предположим, типичный пенсионер потребляет два набора потребительских благ (x1) и (x2). Его предпочтения описываются функцией полезности u(x1, х2) = x1x2. Средний размер пенсии в равен 120 денежных единиц, а цены наборов потребительских благ (x1) и (x2) составляют соответственно:
p1 = 2 и p2 = 1.
А) Какое количество каждого набора потребительских благ потребляет типичный пенсионер?
Б) Правительство вводит программу социальной поддержки, субсидируя 50% стоимости набора благ (x1) для пенсионеров. Как изменится потребительский выбор типичного пенсионера?
В) Экономические советники утверждают, что если отменить стоимостную субсидию, а средства, которые при этом будут сэкономлены на каждом пенсионере, выдать ему же в виде прибавки к пенсии, благосостояние пенсионера возрастет. Подтвердите или опровергните этот тезис.
Ответ
А) Оптимальный набор потребителя должен удовлетворять условию второго закона Госсена:
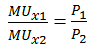
Найдём предельную полезность благ как частные производные от общей полезности:
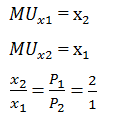
Отсюда
