Задача динамического программирования. Планируется распределение начальной суммы S0 = 80 усл. ед. между четырьмя предприятиями, причем средства выделяются только в размерах, кратных 20 усл. ед.

22 января 2025
Программирование

Условие:

Задача динамического программирования.

Планируется распределение начальной суммы S₀ = 80 усл. ед. между четырьмя предприятиями, причем средства выделяются только в размерах, кратных 20 усл. ед. Предполагается, что выделенные предприятию в начале планового периода средства x приносят прибыль f_k(x).

Считать, что:

1) прибыль f_k(x), полученная от вложения средств в предприятие, не зависит от вложения средств в другие предприятия;

2) прибыль, полученная от разных предприятий, выражается в одинаковых условных единицах;

3) суммарная прибыль равна сумме прибылей, полученных от каждого предприятия.

Функции f_k(x) заданы в таблице:

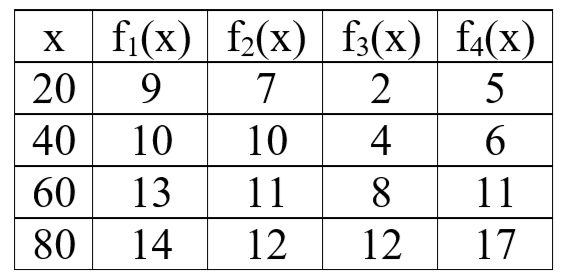
Задание.

1. Определить, какое количество средств нужно выделить каждому предприятию, чтобы суммарная прибыль была наибольшей (используйте принцип оптимальности и уравнения Беллмана).

2. Приведите расчетные таблицы (возможно использование Excel).

3. Опишите особенности модели.

Решение:

Составляем математическую модель задачи. Пусть x_k количество средств, выделенных k-тому предприятию таким образом, что суммарная прибыль F достигает максимума:

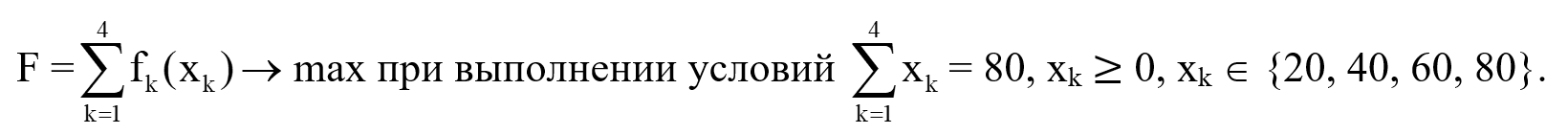
Распределение средств между четырьмя предприятиями рассматривается как четырехшаговый процесс, на каждом шаге которого выделяются средства xk соответствующему предприятию. При этом Sk нераспределенные средства после k-того шага. Первоначал...