1) показать на расчетной схеме реакции опор и определить их величину; 2) составить уравнение поперечной силы Q(х) и изгибающего момента М(х) для всех участков. Построить эпюры изменения поперечной силы Q(х) и изгибающего момента М(х) по длине балки;
- Сопротивление материалов
Условие:
Для заданной расчётной схемы (рис. 2.1) необходимо:
1) показать на расчетной схеме реакции опор и определить их величину;
2) составить уравнение поперечной силы Q(х) и изгибающего момента М(х) для всех участков. Построить эпюры изменения поперечной силы Q(х) и изгибающего момента М(х) по длине балки;
3) из построенной эпюры изгибающего момента М(х) найти его максимальное по модулю значение. Из условия прочности определить размеры поперечного сечения балки и сравнить его по погонной массе с двутавром.
Исходные данные: Р=4 кН; М=7 кН∙м; q=5 кН/м; a=3 м; b=6 м; 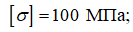 форма сечения: I-й случай – круг, II-й случай – двутавр.
форма сечения: I-й случай – круг, II-й случай – двутавр.
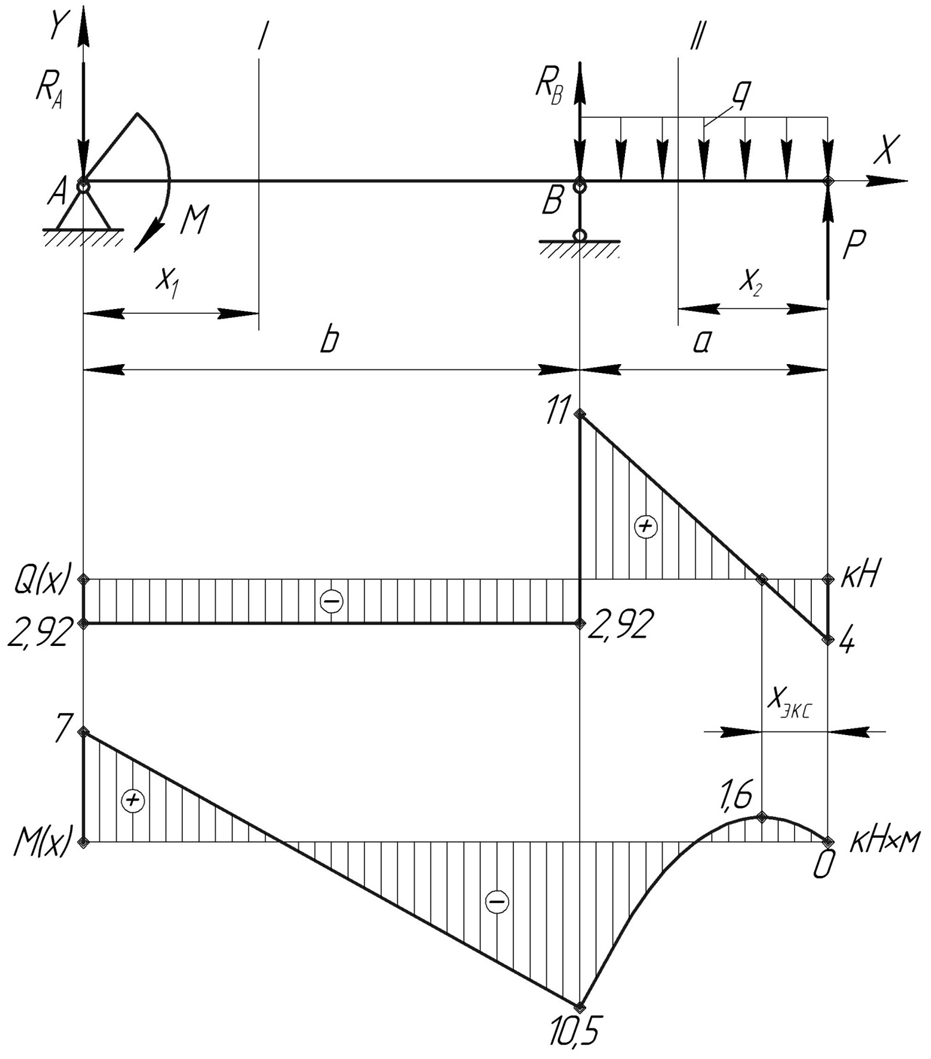
Рис. 2.1. Расчетная схема балки с эпюрами
Решение:
1. Обозначим реакции опор RA и RВ, и определим их величину, используя уравнения равновесия для плоской системы сил:
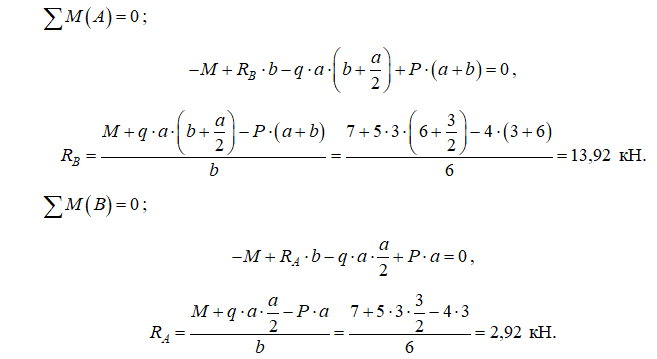
Проверка:
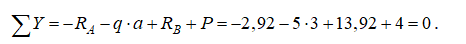
Реакции найдены правильно:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства