Дано: В некоторой частице тела (элемента конструкции типа плиты, оболочки, балки-стенки и др.) задано напряженное состояние в виде тензора напряжений Значения напряжений даны в табл. 1.1 в соответствии с номером варианта, который задается по списку
- Сопротивление материалов
Условие:
Дано:
В некоторой частице тела (элемента конструкции типа плиты, оболочки, балки-стенки и др.) задано напряженное состояние в виде тензора напряжений
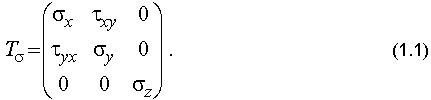
Значения напряжений даны в табл. 1.1 в соответствии с номером варианта, который задается по списку студенческой группы, составленному преподавателем. Значения напряжений заданы формулами:
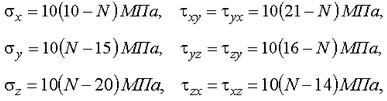
где N - номер варианта.
В задаче 1 напряжения 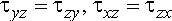 принимаются равными нулю.
принимаются равными нулю.
Требуется:
1. Графически изобразить напряжения на гранях малого элемента тела с учетом их фактических направлений.
2. Определить главные напряжения и направления, пользуясь формулами:
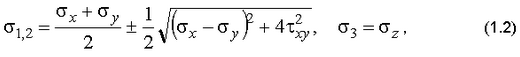

При необходимости перенумеровать главные напряжения в порядке убывания по алгебраической величине:

3. Проверить величины главных напряжений, как напряжений в системе осей 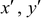 повернутых на угол
повернутых на угол 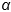 , по формулам:
, по формулам:
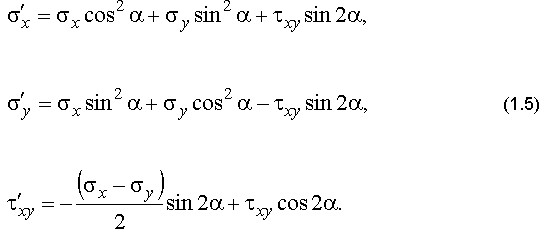
4. Изобразить графически главные площадки и главные нормальные напряжения.
Определить напряжения в системе осей, повернутых на угол 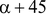 о, подставив в формулы (1.5) вместо
о, подставив в формулы (1.5) вместо 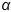 угол
угол 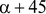 о.
о.
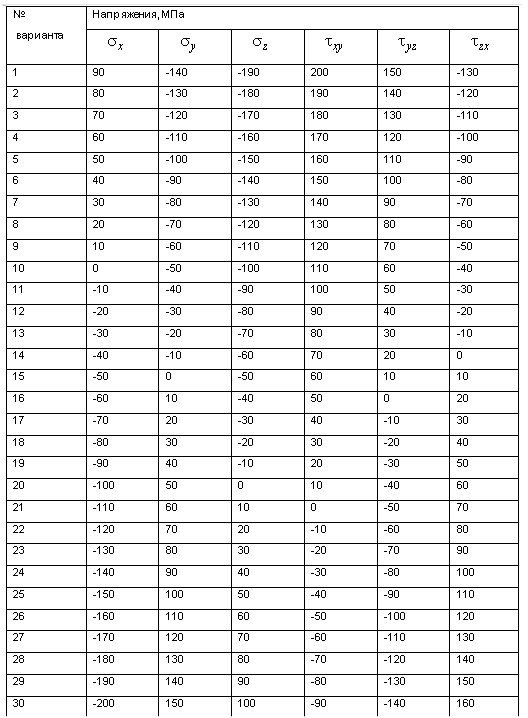
Таблица 1.1
Величины напряжений к задачам 1 и 2
Убедиться в том, что инварианты тензора напряжений сохраняются:
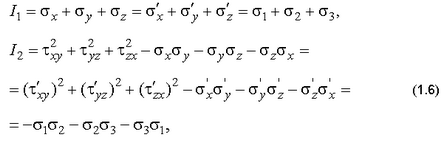
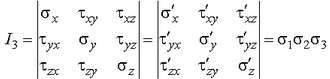
Третий инвариант вычисляется по обычным правилам раскрытия определителя третьего порядка.
Графически изобразить тензор напряжений в виде эллипсоида Ламе. Построить круги напряжений Мора, указать 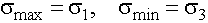 .
.
5. Вычислить главные касательные напряжения
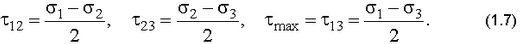
Указать эти величины на кругах Мора и обосновать их инвариантность.
6. Определить среднее нормальное напряжение

и разложить тензор напряжений на шаровой тензор и тензор-девиатор
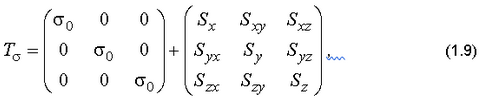
где компоненты тензора-девиатора напряжений вычисляются по формулам
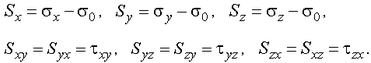
Вычислить на октаэдрических площадках нормальное напряжение

где 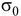 - среднее напряжение, вычисляемое по формуле (1.8), касательное
- среднее напряжение, вычисляемое по формуле (1.8), касательное
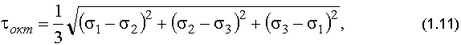
а также интенсивность напряжений
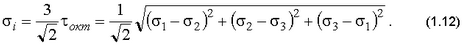
Сравнить 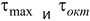 .
.
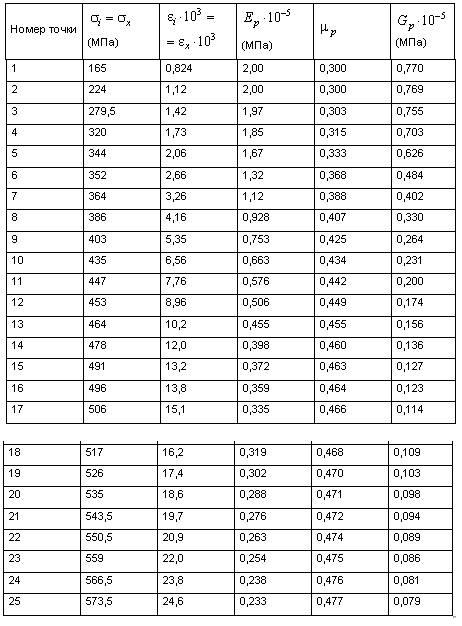
8. Пользуясь данными табл. 1.2 вычислить и занести в таблицу для каждой точки диаграммы 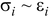 пластический модуль
пластический модуль 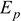 , пластический коэффициент Пуассона
, пластический коэффициент Пуассона 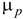 (принимая условие упругого изменения объема), пластический модуль сдвига
(принимая условие упругого изменения объема), пластический модуль сдвига 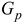 , используя формулы
, используя формулы
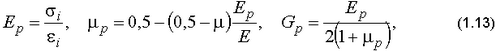
где 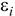 - интенсивность деформаций.
- интенсивность деформаций.
Таблица 1.2
Диаграмма растяжения тонкостенной трубки из стали 45 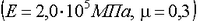
Обосновать, почему при растяжении тонкостенной трубки 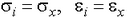 .
.
9. Начертить в масштабе графики зависимостей 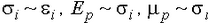 ,
,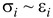 . Определить по графикам предел пропорциональности материала и установить, в каком состоянии (упругом, упругопластическом) находится материал, используя условия пластичности Сен-Венана и Мизеса.
. Определить по графикам предел пропорциональности материала и установить, в каком состоянии (упругом, упругопластическом) находится материал, используя условия пластичности Сен-Венана и Мизеса.
10. Определить деформации пользуясь обобщенным законом Гука для упругого материала
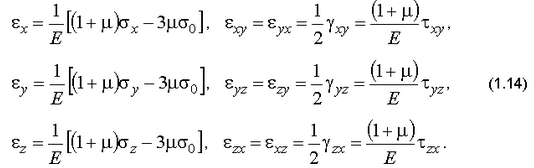
или
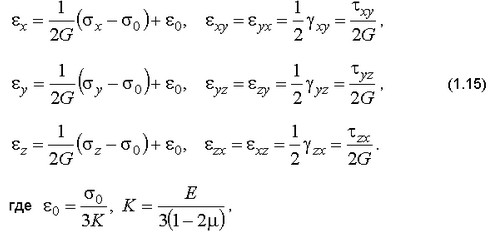
либо соотношениями теории малых упругопластических деформаций (ТМУПД) за пределом упругости
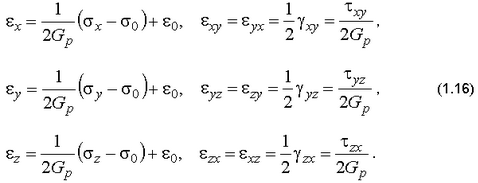
где
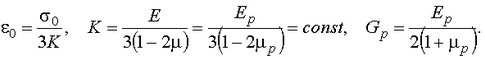
11. Определить главные деформации по формулам
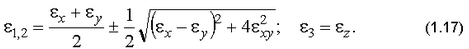
При необходимости перенумеровать главные деформации в порядке убывания по алгебраической величине:

Проверить величины главных деформаций по формулам для упругого материала
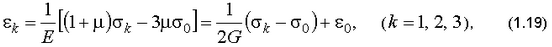
либо упругопластического материала
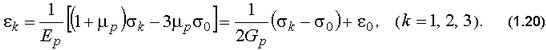
12. Вычислить октаэдрический сдвиг
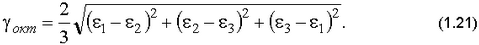
и сравнить его со значением, полученным по формулам
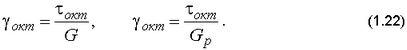
для упругого или упругопластического материала соответственно.
Вычислить главные сдвиги
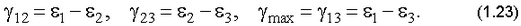
Сравнить величины 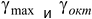 .
.
Решение:
1. Компоненты тензора напряжений (1.1), выбранные в соответствии с номером варианта из табл. 1, имеют следующие числовые значения:
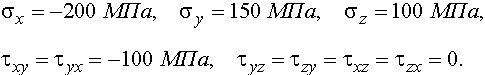
Изображение напряжений с учетом их фактических направлений показано на рис. 1.1.
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства