Условие задачи
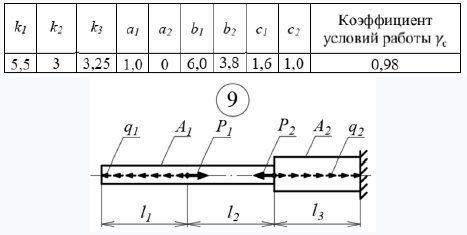
Для ступенчатого прямолинейного бруса, требуется:
1) определить продольные силы N по участкам стержня и построить эпюру;
2) построить эпюру нормальных напряжений σ;
3) построить эпюру продольных перемещений поперечных сечений 
;
4) определить работу внешних сил и внутреннюю потенциальную энергию деформации;
5) из условия прочности подобрать параметр площади поперечного сечения A.
Пункты 1-3 выполнить в общем виде, выразив искомые N, σ и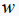 
в долях q, l, E, А.
Принять: длина li = ki · l, интенсивность распределенной нагрузки qi =ai · q, сосредоточенная сила Pi = bi · ql, площадь поперечного сечения Ai = ci · A.
При расчетах принять: интенсивность распределенной нагрузки q =10 кН/м, длина l =1 м, модуль упругости первого рода E = 2*105 МПа, расчетное сопротивление R=300 МПа.
Ответ
Определяем реакцию в опоре А бруса.
𝐹𝑧=0: 𝑅АР1+Р2+𝑞1𝑙1=0;
𝑅А=Р1+Р2+𝑞1𝑙1=60+38+10∙5,5=33кН; 𝑀А=0; 𝑌А=0.
Строим эпюру продольных сил.
Участок DC: 0 DC 𝑙1
𝑁1=𝑞1𝑙1;
𝑁(0)=0кН;
𝑁(5,5)=55кН. (Участок растягивается).
Участок CB: 𝑙1 CB 𝑙1 + 𝑙2:
𝑁2=𝑞1𝑙1Р1.
𝑁(5,5)=5кН;
𝑁(8,5)=5кН. (Участок сжимается).
Участок BA: 𝑙1 + 𝑙2 BA 𝑙1 + 𝑙2 + 𝑙3:
𝑁3=𝑞1𝑙1Р1+Р2.
𝑁(8,5)=33кН;
𝑁(11,75)=33кН. (Участок растягивается).
Определяем нормальные напряжения в необходимых поперечных сечениях стержня при условии
