Для трёхмерного тела заданы три компонента вектора перемещения u, v, w как функции декартовых координат x, y, z. Требуется:

Для трёхмерного тела заданы три компонента вектора перемещения u, v, w как функции декартовых координат x, y, z.

Требуется:

1. Определить компоненты тензора деформаций и тензора напряжений в произвольной точке тела.

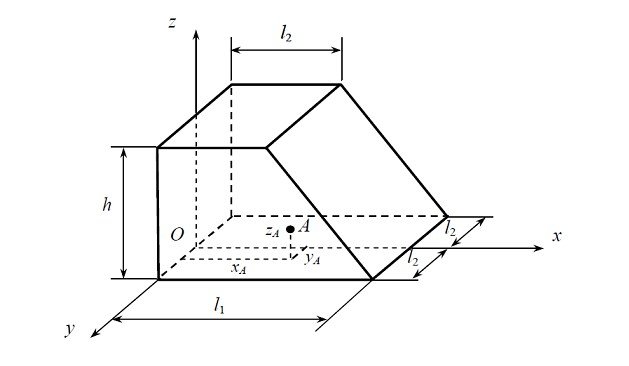
2. Определить компоненты объёмной нагрузки X, Y, Z и поверхностной нагрузки Xν, Yν, Zν на наклонной грани тела.

3. Найти величину относительной объёмной деформации θ₀ и среднего нормального напряжения σ₀ в точке A с заданными координатами x_A, y_A, z_A . Записать тензор напряжений T_н, шаровой тензор Т_ш и девиатор напряжений D_н в этой точке.

4. Определить инварианты тензора напряжений I₁, I₂ , I₃ в точке A , а также величины главных напряжений σ₁, σ₂ , σ₃ и наибольшего касательного напряжения τ_max в этой точке.

5. Определить погрешность вычисления инвариантов тензора напряжений в точке A.

Дано:

а = 1∙10^–3 м^–1; 

b = 2‧10^–3 м^–1; 

c = 3∙10^–3 м^–1;

α = 0,5 м; 

Е = 2∙10⁵ МПа; 

ν = 0,25; 

l₁ = 0,5 м; 

l₂ = 0,3 м; 

h = 0,3 м;

х_А = 0,1 м; 

у_А = 0,1 м; 

z_А = 0,2 м;

у_А = 0,1 м; 

z_А = 0,2 м;