Условие:
К стальному валу (Рис. 1) приложены три известных крутящих момента: М1, М2, M3.
Требуется:
1) установить, при каком значении крутящего момента Х угол закручивания правого концевого сечения вала равен нулю;
2) для найденного значения Х построить эпюру крутящих моментов;
3) при найденному значении τ определить диаметр вала из расчета на прочность;
4) найти наибольший относительный угол закручивания θ, 0/м.
Исходные данные:
a=2 м; b=1,7 м; c=1,2 м; М1=2,4 кН·м; М2=1,7 кН·м; М3=1,8 кН·м; [τ]=80 МПа; G=8∙104 МПа.

Решение:
1) Раскроем статическую неопределимость вала из условия, что полный угол его закручивания равен нулю.
Разделим вал на четыре участка и пронумеруем их справа-налево.
Составим уравнение полного угла закручивания вала
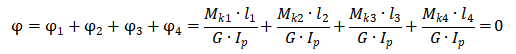
Подставив в уравнение крутящие моменты и длины участков, получим
