1. Перед вами сто пар чисел (Х,У) – статистический ряд объёма n =100. Упорядочите по возрастанию каждый признак в отдельности. Данные запишите в таблицу и дайте ей номер1.
- Статистика
Условие:
1. Перед вами сто пар чисел (Х,У) – статистический ряд объёма n =100. Упорядочите по возрастанию каждый признак в отдельности. Данные запишите в таблицу и дайте ей номер1.
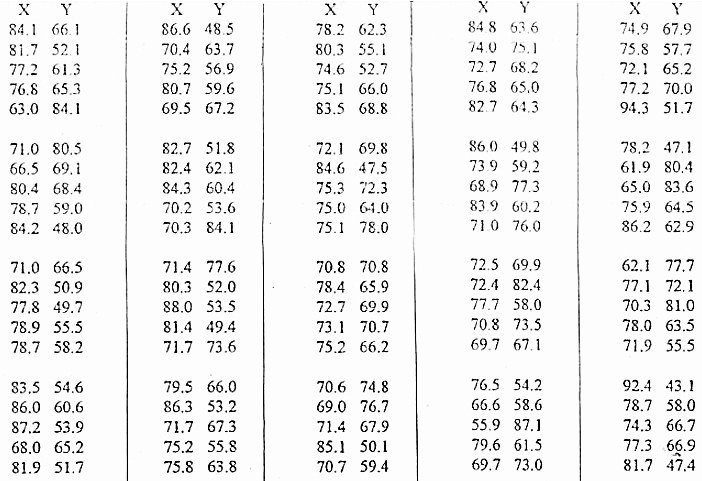
2. Запишите минимальное и максимальное значения совокупности Х и У (статистического ряда):
3. Найдите размах варьирования каждого измеримого признака:
4. Подсчитайте число интервалов по формуле Стьюргесса:
Замечание: Напомним, что число интервалов может быть выбрано произвольно. Можно выбрать различное число интервалов для совокупностей Х и У (например, для совокупности Х число интервалов равно 6, а для совокупности У - 7). Выбор r зависит от объёма n, размаха R и от цели статистического исследования. Принято, чтобы получилось не менее 6 и не более 20 интервалов.
5. Определите, чему равен шаг варьирования каждого признака (длина интервала будущего вариационного ряда для Х и для У). Имейте в виду, т.к. значения Х и У не одинаковые, то и значения размаха варьирования, шага варьирования и пр. у них – разные.
6. Теперь найдем границы интервалов каждого признака таким образом, чтобы минимальное значение стало серединой первого интервала, а максимальное – серединой последнего. Для этого отступим от 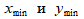 на полшага, а к правому концу каждого интервала будем прибавлять длину шага:
на полшага, а к правому концу каждого интервала будем прибавлять длину шага:
7. Найдем середины получившихся интервалов:
О верности подсчетов свидетельствует равенство (возможно приближенное) последних, восьмых, значений соответственно 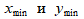
8. Постройте корреляционное поле: в двумерной системе координат оси ОХ и ОУ разбиваются на интервалы длиной 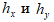 . За начало координат возьмите точку , т.е. начальные значения интервалов. Через границы интервалов
. За начало координат возьмите точку , т.е. начальные значения интервалов. Через границы интервалов 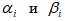 проводятся прямые, параллельные осям,- получают «сетку» из промежутков, в которую вносят (отмечают) исходные сто пар точек (х,у). Условимся, что при попадании какой-нибудь точки (х,у) на линию сетки, её относят к правому или верхнему квадрату. Обозначьте корреляционное поле таблицей 2.
проводятся прямые, параллельные осям,- получают «сетку» из промежутков, в которую вносят (отмечают) исходные сто пар точек (х,у). Условимся, что при попадании какой-нибудь точки (х,у) на линию сетки, её относят к правому или верхнему квадрату. Обозначьте корреляционное поле таблицей 2.
9. Заполните корреляционную таблицу абсолютных частот:
Таблица 3
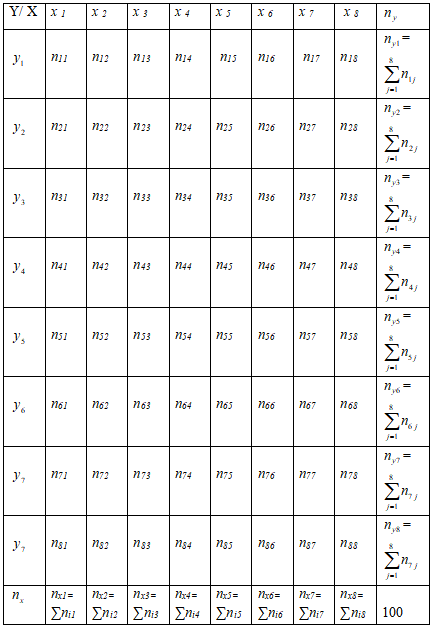
в строках указываем середины 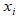 интервалов
интервалов 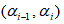 , в столбцах – середины
, в столбцах – середины 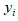 интервалов
интервалов 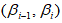 , а в соответствующую ячейку таблицы записываем число точек
, а в соответствующую ячейку таблицы записываем число точек 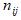 , попавших в аналогичную
, попавших в аналогичную 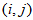 -ую ячейку сетки корреляционного поля (смотрите пример).
-ую ячейку сетки корреляционного поля (смотрите пример).
10. С помощью корреляционной таблицы частот, получите и выпишите отдельно вариационные ряды составляющих Х и У.
11. Заполните таблицу «Статистическая совокупность» для каждого признака в отдельности:
Таблица 6
Статистическая совокупность измеримого признака Х
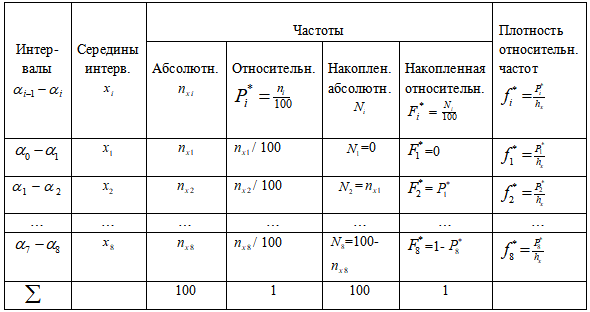
Сделать это очень просто: с помощью пунктов 6, 7 и 10 заполняем первые три столбца таблицы; данные в остальные столбцы вписываем после подсчета соответствующей формулы, записанной в ячейке таблицы.
Теперь составьте такую же таблицу для признака У, получите таблицу 7.
1. По данным таблицы 6 ( для признака У – таблицы 7), постройте:
а) полигон и гистограмму распределения – графические оценки плотности распределения вероятностей генеральной совокупности;
б) полигон накопленных частостей – график эмпирической функции распределения:
Решение:
1. Упорядочим данные в порядке возрастания, получим следующую таблицу:
Таблица 1
Статистический ряд. Упорядоченные значения величин
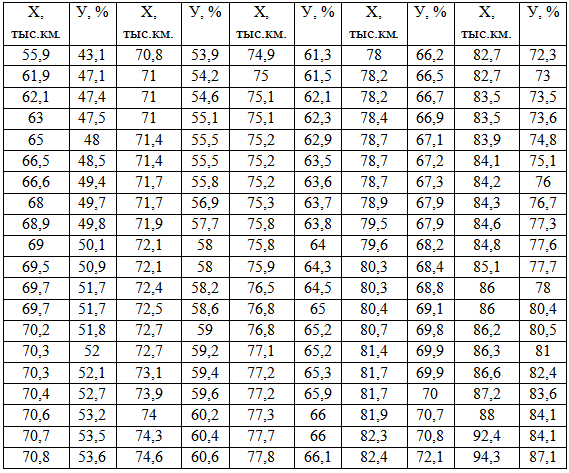
![]()
2. Размах варьирования:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства