Условие задачи
1.Используя данные «Российского статистического ежегодника. 2017 г.», выберете 2-а взаимосвязанных признака (факторный и результативный) по 10-и субъектам РФ 2016 г.
2.Упорядочите выбранную информацию по факторному признаку. Проанализируйте результаты группировки. Исключите аномальные наблюдения, если они имеются.
4.Постройте эмпирическую линию регрессии.
5.Выберете математическую функцию для построения уравнения регрессии.
6.Определите с помощью метода наименьших квадратов параметры уравнения регрессии.
7.Определите теоретические значения результативного признака.
8.Изобразите на графике фактических данных теоретическую кривую. Оцените визуально выбор функции связи.
9.Определите среднюю относительную ошибку аппроксимации. Оцените ее значение.
10.Определите индекс корреляции (теоретическую и корреляционное отношение). Произведите оценку показателя.
11.Определите линейный коэффициент парной корреляции (если связь линейная).
12.Определите коэффициенты Фехнера и Спирмена. Проанализируйте рассчитанные показатели.
Ответ
Таблица - Исходные данные
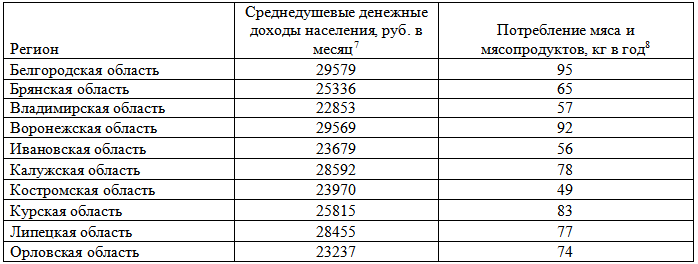
По формуле Стерджесса определяем число групп в образующихся интервальный ряд
N=1+3.322lgN
Где N=10 в соответствии с условием задачи
N=1+3.322lg10=4,34 группы
Принимаем группировку с равными интервалами и определяем величину интервала h по формуле
