Условие:
1. Для каждой участвующей в таблице одномерной случайной величины X и У (сокращенно СВ х и СВ у) построить:
а)вариационный и центрированный интервальный ряды распределения частот и относительных частот наблюдаемых значений СВ х и СВ у.
б) гистограмму и полигон полученных относительных частот СВ х и СВ у;
2. Для каждой участвующей в таблице одномерной случайной величины X и У вычислить:
а)выборочные средние 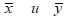
б)выборочные дисперсии 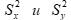
в)выборочные средние квадратичные отклонения 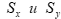
3. Найти точечные оценки параметров нормального закона распределения, предполагая, что исследуемые СВ х и СВ у распределены по нормальному закону; записать их дифференциальную (плотность вероятности) и интегральную функции распределения.
4. Провести корреляционный анализ данных, для чего:
а) составить корреляционную таблицу;
б) найти по данным корреляционной таблицы выборочный коэффициент корреляции 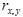
в) построить корреляционное поле;
г) по характеру расположения точек корреляционного поля подобрать общий вид функции регрессии;
д) найти эмпирические функции регрессии у на х и х на у.
е) построить их графики.
Для контроля приведены значения коэффициента Пирсона:
Вариант 24
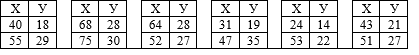
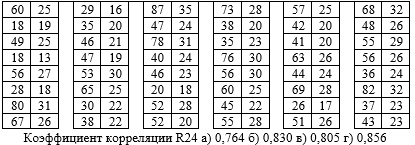
Решение:
Упорядочим каждый ряд значений переменных Х и У по возрастанию:
Таблица 1. - Ранжированные ряды.

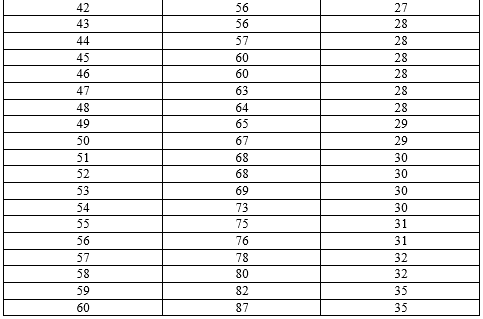
1)Построим интервальные вариационные ряды:
При построении ряда с равными интервалами величина интервала h ...
