Из генеральной совокупности извлечена выборка, которая представлена в виде интервального вариационного ряда а) Предполагая, что генеральная совокупность имеет нормальное распределение, построить доверительный интервал
- Статистика
Условие:
Из генеральной совокупности извлечена выборка, которая представлена в виде интервального вариационного ряда
а) Предполагая, что генеральная совокупность имеет нормальное распределение, построить доверительный интервал для математического ожидания с доверительной вероятностью у=0,95.
б) Вычислить коэффициенты асимметрии и эксцесса, используя упрошенный метод вычислений, и сделать соответствующие предположения о виде функции распределения генеральной совокупности
в) Используя критерий Пирсона, проверить гипотезу о нормальности распределения генеральной
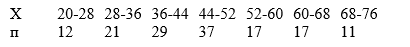
Решение:
Вычислим относительные частоты по формуле и все вычисления запишем в таблицу, т.е. построим вариационный ряд относительных частот:
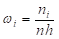
В данном случае
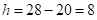
Получим следующий интервальный ряд:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства