Известно, что признак распределен по одному из трех законов: равномерному, показательному или нормальному. Над признаком провели испытания. Выяснить закон распределения признака.
- Статистика
Условие:
Известно, что признак распределен по одному из трех законов: равномерному, показательному или нормальному. Над признаком провели испытания. Выяснить закон распределения признака.
1. Построить статистическое распределение (интервальный статистический ряд), гистограмму.
2. Найти числовые характеристики выборки (минимум: выборочное среднее, дисперсию, среднее квадратическое отклонение, исправленные выборочные дисперсию и среднее квадратическое отклонение).
3. Сформулировать статистическую гипотезу о виде закона распределения.
4. Найти параметры распределения сформулированной гипотезы.
5. Проверить статистическую гипотезу о виде закона распределения с найденными параметрами (с помощью критерия Пирсона).
6. Сделать вывод о законе распределения исследуемого признака.
Исходные данные:
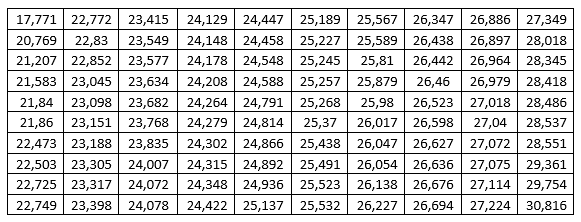
Решение:
Обозначим исследуемый признак X
Построим статистическое распределение (интервальный статистический ряд), гистограмму.
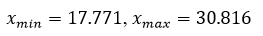
Размах
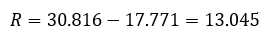
Количество интервалов для группировки определим по формуле Стерджесса:
Объем в...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства