На основании данных обследования кредитов, выданных банком: Данные выборочного обследования ссуд, выданных банком физическим лицам в течение квартала (в графах «Вид ссуды»: А – автокредитование, И – ипотечное кредитование, Л – кредитование для любых
- Статистика
Условие:
На основании данных обследования кредитов, выданных банком:
Данные выборочного обследования ссуд, выданных банком физическим лицам в течение квартала
(в графах «Вид ссуды»: А – автокредитование, И – ипотечное кредитование, Л – кредитование для любых целей; «Сумма» – размер ссуды в тыс. руб.)
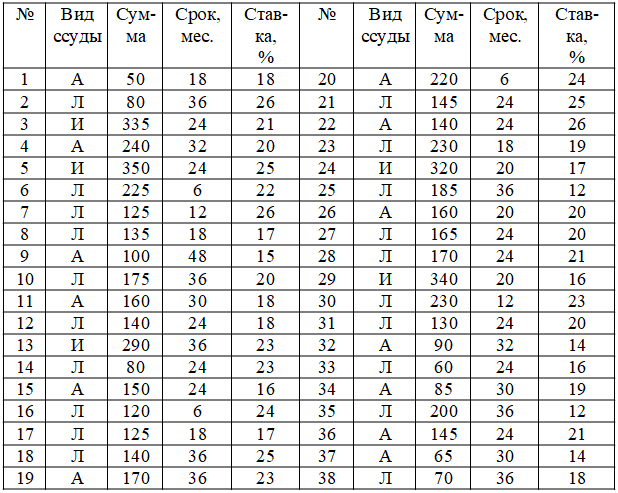
1. Провести группировку выданных ссуд по сроку с равными интервалами и оптимальным числом групп и представить полученные данные в виде статистического ряда распределения. На основе полученного ряда построить гистограмму и кумуляту распределения ссуд по сроку.
2. Составить и назвать статистическую таблицу с перечневым подлежащим и сложным сказуемым, сгруппированным по двум количественным признакам. Количество групп и подгрупп в сказуемом – произвольное.
3. Сгруппировать ссуды: а) по виду и б) по ставке на 5 групп с равными интервалами. Определить относительные показатели структуры для каждой группировки. Рассчитать размер средней ссуды для каждой группы первой группировки и ее среднюю ставку в каждой группе второй.
4. Исчислить по сгруппированным выше данным (пункт 3а) средний размер выданных ссуд с помощью следующих средних (простых и взвешенных): а) арифметической; б) гармонической.
5. Рассчитать показатели вариации ставки ссуд: а) по сгруппированным выше данным (пункт 3б) с использованием средней арифметической простой и взвешенной; б) по не сгруппированным данным.
6. Определить модальные и медианные значения срока ссуд а) по не сгруппированным данным; б) из статистического ряда распределения (пункт 1) аналитически и графически.
7. Вычислить параметры линейного уравнения регрессии для зависимости срока ссуд от их размера. Определить тесноту связи между признаками с помощью коэффициента корреляции знаков (коэффициента Фехнера).
Решение:
1. Оптимальное число групп определим по формуле Стержессома:
m=1+3.322*lgN=1+3.322lg38=7
Величина равного интервала находится по формуле:
i=(xmax-xmin)/m=(48-6)/7= 6 мес.
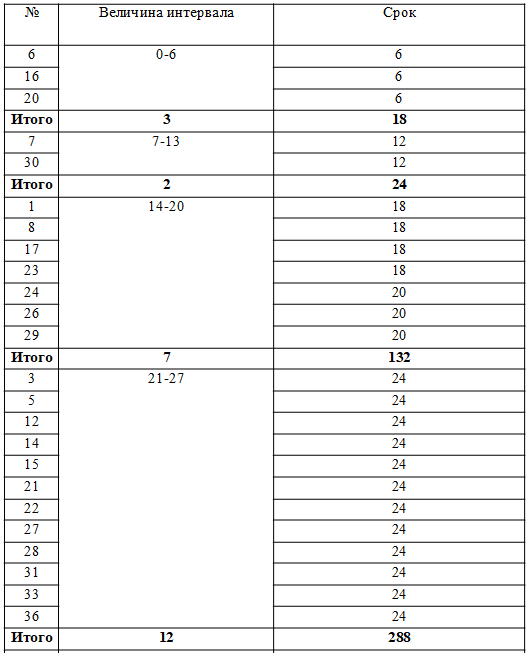
Группировку ссуд по сроку представлена в таблице 1.
Таблица 1. Группировка выданных ссуд по сроку, мес.
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства