На основе структурной группировки построить вариационный частотный и кумулятивный ряды распределения, используя закрытые интервалы, приняв количество 5. Результаты представить в виде таблицы и изобразить графически.
- Статистика
Условие:
На основе данных выполнить:
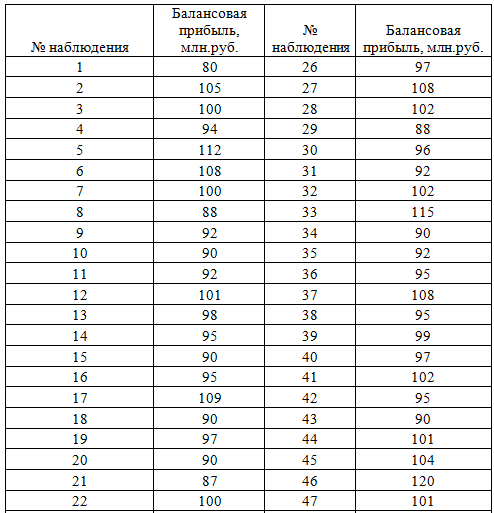

1. На основе структурной группировки построить вариационный частотный и кумулятивный ряды распределения, используя закрытые интервалы, приняв количество 5. Результаты представить в виде таблицы и изобразить графически.
2. Проанализировать вариационный ряд распределения, вычислить:
- среднее арифметическое значение признака;
- моду и медиану аналитически и графически;
- дисперсию и среднеквадратическое отклонение;
- размах вариации и коэффициент вариации.
3. Полагая, что данные получены при помощи собственно – случайного 10-ти процентного бесповторного оборота, определить:
- пределы, за которые с вероятностью 0,99 не выйдет среднее значение признака, рассчитанное по выборочной совокупности;
- как нужно изменить объем выборки, чтобы увеличить вычислений предельной ошибки средней величины в 3 раза.
4. Не учитывая вычисления пункта 3, и полагая, что данные получены при помощи повторного отбора, определить:
- как изменить объем выборки, чтобы снизить предельную ошибку в 3 раза.
Решение:
1. Принимаем группировку с равными интервалами и определяем величину интервала h по формуле
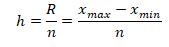
тогда имеем
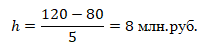
В соответствии с найденными параметрами строим интервальный ряд распределения. Группировка предста...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства