Главная
Библиотека
Статистика
Определить по первичным данным: квартили; показатель квартильной вариации; моду, среднюю арифметическую. Построить интерва...

Определить по первичным данным: квартили; показатель квартильной вариации; моду, среднюю арифметическую. Построить интервальный ряд распределения

«Определить по первичным данным: квартили; показатель квартильной вариации; моду, среднюю арифметическую. Построить интервальный ряд распределения»

29 января 2025
Статистика

Условие:

Имеются данные о количестве бракованных изделий в цехе по рабочим дням месяца (табл 3,43)

Таблица 3.43

1. Определить по первичным данным:

а)квартили; б) показатель квартильной вариации; в ) моду, среднюю арифметическую;

2. Построить интервальный ряд распределения и определить:

а) среднюю арифметическую, моду и медиану; сравнить показатели центра распределения по несгруппированным данным;

б) среднее квадратическое отклонение и коэффициент вариации, сделать вывод;

в) степень ассиметрии распределения, использовав показатель, основанный на характеристиках центра распределения;

г) удельный вес числа дней, в которые количество бракованных изделий не выходит за пределы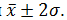

Решение:

1. Определим по первичным данным:

а) квартили; б) показатель квартильной вариации; в ) моду, среднюю арифметическую;

Квартили это значения признака в ранжированном ряду распределения, выбранные таким образом, что 25% единиц совокупности будут меньше по величине Q₁, 25% будут заключены между Q₁ и Q₂, 25% - между Q₂ и Q₃. Остальные 25% превосходят Q₃.

Находим 1/4 ранжированного ряда: Ранжированный ряд включает четное число единиц, следовательно квартиль Q1 определяется как среднее из двух значений: (7 + 8)/2 = 7.5