Условие:
По данным, представленным в таблице, выполните корреляционно-регрессионный анализ зависимости между двумя признаками X и Y в соответствии с вариантом, указанным преподавателем:
1) определите линейную модель регрессии, дайте интерпретацию ее параметров;
2) рассчитайте показатели тесноты связи между признаками (индекс корреляции, линейные коэффициенты корреляции и детерминации), сделайте выводы по их значениям;
3) проверьте статистическую значимость полученной модели регрессии и коэффициента корреляции на основе применения статистических критериев Стьюдента и Фишера;
4) выполните анализ качества полученной модели и пригодности ее для прогнозирования;
5) выполните прогноз значения результативной переменной Y на основе модели регрессии, приняв ожидаемое значение факторной переменной Х, равное среднему значению этого признака по результатам наблюдений;
6) изобразите графически исследуемую зависимость, построив поле корреляции и график линии регрессии, выведите на поле графика уравнение регрессии и коэффициент детерминации (показатель достоверности аппроксимации).
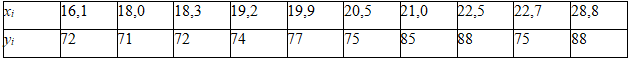
Решение:
1. Определим линейную модель регрессии и дадим интерпретацию ее параметров.
Для расчета параметров регрессии построим расчетную таблицу (табл. 1)
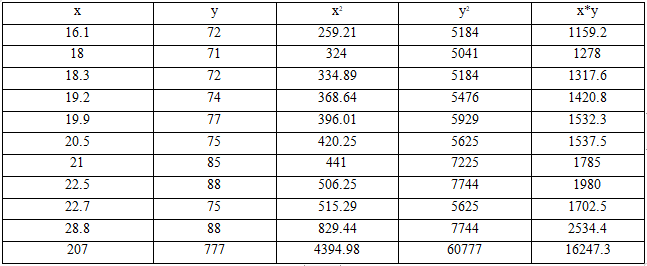
Параметры регрессии a и b можно найти по формуле, найдя ранее необходимые показатели:
