По заданному варианту выборочной совокупности независимых и равноточных измерений случайной величины Х(СВХ) вычислить точечные оценки для математического ожидания, среднеквадратического отклонения, коэффициента асимметрии.
- Статистика
Условие:
По заданному варианту выборочной совокупности независимых и равноточных измерений случайной величины Х(СВХ)
(предварительно удалив резко выделяющиеся наблюдения):
1. Вычислить точечные оценки для математического ожидания, среднеквадратического отклонения, коэффициента асимметрии.
2. Составить интервальный статистический ряд распределения относительных частот и построить гистограмму и полигон относительных частот.
3. Найти эмпирическую функцию распределения и построить ее график.
4. Исходя из общих представлений о механизме образования СВ X, а также по виду гистограммы и полигона относительных частот и вычаленным числовым характеристикам, выдвинуть гипотезу о виде распределения СВ X, записать плотность распределения вероятностей и функцию распределения для выдвинутого гипотетического закона, заменяя параметры закона вычисленными для них оценками.
5. По критерию согласия х2 Пирсона проверить соответствие выборочного распределения гипотетическому закону для уровня значимости q=0,05.
6. Вычислить интервальные оценки для математического ожидания m и среднеквадратического отклонения, соответствующие доверительным вероятностям 0,95 и 0,99.
Таблица 1. Данные о месяце рождения студентов 1 курса ф-та ФЭУ ВолгГТУ приведены в таблице
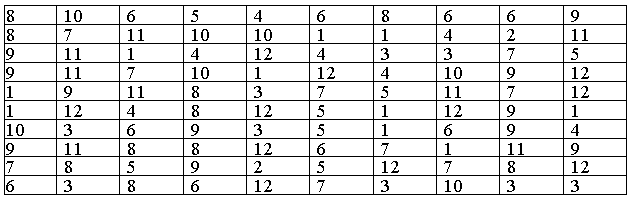
Решение:
Преобразуем значения исходных данных.
Таблица 2.

Объем выборки равен 100. Составим таблицу вспомогательных вычислений.
Таблица 3.
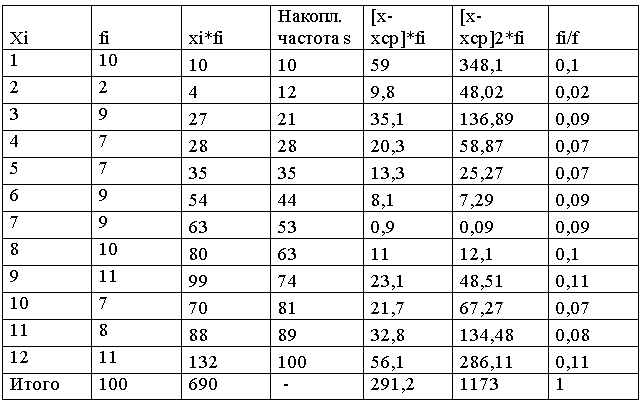
1. Вычислим точечные оценки для математического ожидания, среднеквадратиче...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства