Условие задачи
По заданному варианту выборочной совокупности независимых измерений случайной величины Х (СВ Х) (предварительно удалив резко выделяющиеся наблюдения):
1. Составить интервальный статистический ряд распределения относительных частот, построить гистограмму и полигон относительных частот
2. Найти эмпирическую функцию распределения и построить ее график
3. Вычислить точечные оценки для математического ожидания, дисперсии, коэффициентов асимметрии и эксцесса
4. Исходя из общих представлений о механизме образования СВ Х, а также по виду гистограммы и полигона относительных частот и вычисленным числовым характеристикам, выдвинуть гипотезу о виде закона распределения СВ Х; записать плотность распределения вероятностей и функцию распределения для выдвинутого гипотетического закона, заменяя параметры закона вычисленными для них оценками
5. Вычислить интервальные оценки для математического ожидания и дисперсии, соответствующие доверительным вероятностям р = 0,95 и р = 0,99.
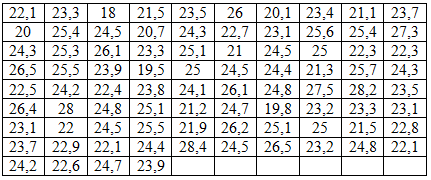
В таблице приведены данные о месячной зарплате рабочих одного из предприятий, в тыс. руб.
Ответ
1) Сгруппируем исходные данные, то есть разобьем их на k частичных интервалов (xi , xi+1 ], i=1, 2,, k, и посчитаем частоту попадания наблюдаемых знаний в частичные интервалы.
Для нашего примера: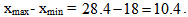 
Этот отрезок удобно разбить на 8 интервалов длины h = 1,3. Результаты промежуточных расчетов приведены в таблице
