Условие задачи
СВ имеет гауссовское распределение.
а) Постройте двусторонние доверительные интервалы уровня надежности 0,99 для математического ожидания и дисперсии наблюдаемой случайной величины.
б) Проверьте на уровне значимости 0,05 гипотезу о том, что математическое ожидание наблюдаемой СВ равно 0, а дисперсия равна 400.
Исходные данные:
- выборочное среднее (оценка математического ожидания),
- исправленная дисперсия,
- исправленное среднее квадратическое отклонение,
n=190 – объем выборки.
Ответ
а) Доверительный интервал для генерального среднего.
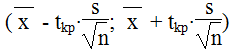
Поскольку n30, то определяем значение tkp по таблицам функции Лапласа.
В этом случае 2Ф(tkp) =
По таблице функции Лапласа найдем, при каком tkp зн...
Потяни
