1. Главная
  2. Библиотека
  3. Статистика
  4. Произведена выборка 80 деталей из текущей продукции токарного автомата. Проверяемый размер деталей X измерен с точностью д...

Произведена выборка 80 деталей из текущей продукции токарного автомата. Проверяемый размер деталей X измерен с точностью до одного миллиметра. Результаты измерений приведены в таблице. 1) Построить статистическое распределение выборки.

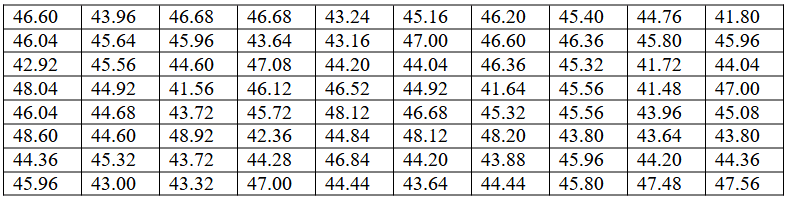
«Произведена выборка 80 деталей из текущей продукции токарного автомата. Проверяемый размер деталей X измерен с точностью до одного миллиметра. Результаты измерений приведены в таблице. 1) Построить статистическое распределение выборки.»
  • Статистика

Условие:

Произведена выборка 80 деталей из текущей продукции токарного автомата. Проверяемый размер деталей X измерен с точностью до одного миллиметра. Результаты измерений приведены в таблице.

Построить статистическое распределение выборки.

Выполнить точечные оценки среднего значения и дисперсии случайной величины

Построить гистограмму относительных частот, установив статистический (эмпирический закон распределения). 

На том же чертеже построить кривую нормального распределения с параметрами и и проанализировать, хорошо ли статистические данные описываются нормальным законом распределения.

Решение:

Минимальное значение выборки
xmin = 41,48 мм.

Максимальное значение выборки

xmax = 48,92 мм.

Размах выборки

R = xmax xmin = 7,44 мм.

Количество интервалов статистического распределения выборки определяя-ется по правилу Стерджеса

n = 1 + [3,322 lg N] = 1 + [3,322 lg 80] = 7.

Размер интервала

= R/n = 1,06 мм.

Распределив значения размера детали по интервалам, запишем результаты

измерений в таблицу. Там же укажем середины интервалов xi, частоты ni и относительные частоты wi.

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я