Проведены наблюдения над некоторыми статистическими показателями. Зафиксированы их значения и сформированы выборки (представлены в таблице по вариантам).

Проведены наблюдения над некоторыми статистическими показателями. Зафиксированы их значения и сформированы выборки (представлены в таблице по вариантам). 

Требуется по данным выборочной совокупности провести обработку статистических данных, начальный анализ и сделать выводы:

1.  Составить вариационный ряд частот и частостей.

2.   Изобразить полигон частот. Сделать обоснованное предположение о законе распределения.

3.  Составить и изобразить эмпирическую функцию распределения

4. Вычислить основные числовые характеристики выборки: размах, мода, медиана, выборочное среднее значение, выборочная дисперсия, выборочное среднеквадратическое отклонение, асимметрия, эксцесс. Интерпретировать результаты вычислений. Сделать обоснованные выводы о законе распределения.

5.  По этой выборке найти точечные оценки для математического ожидания М(Х) и среднеквадратического отклонения 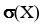генеральной совокупности

6. Найти интервальные оценки для математического ожидания М(Х) и  среднеквадратического отклонения 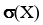генеральной совокупности при следующих условиях: доверительный интервал для математического ожидания М(Х) с надёжностью 90%; доверительный интервал для среднеквадратического отклонения 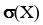с надёжностью 95%.

Данные выборок