Условие задачи
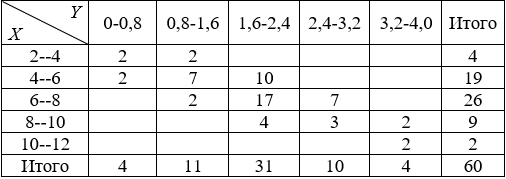
Распределение 60 предприятий по объему инвестиций в развитие производства X (млн.руб.) и получаемой за год прибыли Y (млн.руб.) представлены в таблице:
1) вычислить групповые средние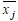 
и 
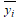, построить эмпирические линии регрессии;
2) предполагая, что между переменными X и Y существует линейная корреляционная зависимость:
а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать содержательную интерпретацию полученных уравнений;
б) вычислить коэффициент корреляции, на уровне значимости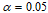 
оценить его значимость и сделать вывод о тесноте и направлении связи между переменными X и Y;
в) используя соответствующее уравнение регрессии, оценить полученную прибыль при объеме инвестиций 5 млн. руб.
Ответ
1) Полученные в ходе обследования эмпирические данные представляют собой двумерную выборку, объем которой равен 60. По каждой переменной они представляют собой интервальный вариационный ряд. Для упрощения дальнейшей обработки заменим интервальные вариационные ряды их дискретными аналогами. Для этого каждый интервал разбиения, как по переменной X, так и по переменной Y , будем характеризовать их срединным значением, для этого вычислим середины каждого интервала. Обозначим варианты переменной X через , а варианты переменной Y через . Получим:
