Разбить исходные ряды на две выборки – зависимую и независимую. В качестве независимой выборки взять часть ряда за 4-5 последних лет. Значения ряда за предыдущее время будут зависимой выборкой.
- Статистика
Условие:
Разбить исходные ряды на две выборки – зависимую и независимую. В качестве независимой выборки взять часть ряда за 4-5 последних лет. Значения ряда за предыдущее время будут зависимой выборкой.
Для зависимой выборки:
1. Рассчитать ВКФ для ТПО и R.
2. Рассчитать уровни значимости ВКФ.
3. Построить совмещенный график ВКФ и уровней значимости.
4. Определить прогностическое направление ТПО = f (R) и в этом направлении выявить оптимальную заблаговременность прогноза ТПО.
5. Сформулировать уравнение регрессии (модели) ТПО = f (R) с оптимальной заблаговременностью.
6. Сформировать ряды (с учетом сдвигов), необходимые для расчета модели.
7. Рассчитать все характеристики модели: коэффициенты модели и 4 параметра качества.
8. На основе полученных коэффициентов написать уравнение прогностической модели. Оценить ее качество (качество зависимого прогноза).
Для независимой выборки:
9. Рассчитать по уравнению прогностической модели значения ТПО в моменты времени независимой выборки.
10. Определить стандартную ошибку независимого прогноза. Оценить качество независимого прогноза.
11. Сделать общий вывод о возможности и качестве прогноза ТПО = f (R) с рассмотренной заблаговременностью.
12. Рассчитать значения исследуемой характеристики (например, ТПО) по модели для зависимой и независимой выборок. Построить совмещенный график фактических и рассчитанных по модели значений характеристики для зависимой и независимой выборок одновременно. Проанализировать его.
Исходные данные:
Температура поверхности океана (среднемесячная) с января 1981 по декабрь 2020 в точке с координатами 42,0 с. широты и 49,8 в. долготы- Каспий
Решение:
Среднемесячная ТПО.
Зависимая выборка это наблюдения с января 1981 по декабрь 2015 года. Независимая выборка - наблюдения с января 1916 по декабрь 2020 года.
Коэффициент взаимной корреляции определяется по формуле:
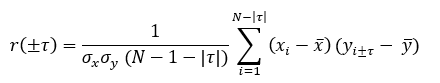
На основе коэффициентов корреляции на каждом сдвиге в обоих направлениях построим ВКФ. После рассчитаем критические значения rкр.
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства